
分析 (1)计算判别式的值得到△=(m-2)2+4,利用非负数的性质得△>0,然后根据判别式的意义可判断方程总有两个不相等的实数根;
(2)令m=2时,则方程化为x2+2x=0,然后利用因式分解法解方程.
解答 (1)证明:△=m2-4(m-2)=m2-4m+8=(m-2)2+4,
∵(m-2)2≥0,
∴△>0,
∴方程总有两个不相等的实数根;
(2)解:当m=2时,
原方程为x2+2x=0,
解得:x1=0,x2=-2.
点评 本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:选择题
 如图,数轴上的点A、B、C、D、E表示连接的五个整数,若点A、E表示的数分别为x、y,且x+y=2,则点C表示的数为( )
如图,数轴上的点A、B、C、D、E表示连接的五个整数,若点A、E表示的数分别为x、y,且x+y=2,则点C表示的数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=x+1与抛物线y=x2+bx+c交于A,B(4,5)两点,点A在x轴上.
如图,在平面直角坐标系中,直线y=x+1与抛物线y=x2+bx+c交于A,B(4,5)两点,点A在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
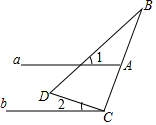 如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠2=60°,则∠B的度数为( )
如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠2=60°,则∠B的度数为( )| A. | 20° | B. | 40° | C. | 30° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com