
【题目】如图,已知![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() ,点
,点![]() 在射线
在射线![]() 上运动(
上运动(![]() 点与
点与![]() 三点不重合),设
三点不重合),设![]() ,
,![]() ,
,![]() .
.

(1)如果点![]() 在
在![]() 两点之间运动时,
两点之间运动时,![]() 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;
(2)如果点![]() 在
在![]() 两点之外运动时,
两点之外运动时,![]() 之间有何数量关系?(只需写出结论,不必说明理由)
之间有何数量关系?(只需写出结论,不必说明理由)
【答案】(1)γ=α+β(2)详见解析
【解析】分析:(1)过点P作P作PF∥l1因为l1//l2则l2//PF,根据两直线平行,内错角相等即可证明γ=α+β,(2) 过点P作P作PF∥l1因为l1//l2则l2//PF,根据两直线平行,内错角相等进行角度转化再根据三角形外角性质可证明∠β=∠γ+∠α,同理可得,当点P在AN上运动时,∠α=∠γ+∠β.
(1)证明:过点P作l3//l1,
∵l1//l2,
∴l2//l3,
∴γ=α+β.
(2)点P在射线AN上时:γ=α-β,
点P在射线BM上时:γ=β-α.
证明:过点P作l3//l1,
∵l1//l2,
∴l2//l3,
∴γ=α+β.
详解:(1)∠γ=α+∠β,
理由:过点P作PF∥l1(如图1),
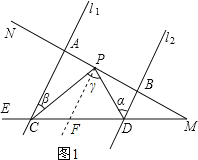
∵l1∥l2,
∴PF∥l2,
∴∠α=∠DPF,∠β=∠CPF,
∴∠γ=∠DPF+∠CPF=α+∠β,
(2)当点P在MB上运动时(如图2),

∵l1∥l2,
∴∠β=∠CFD,
∵∠CFD是△DFP的外角,
∴∠CFD=∠α+∠γ,
∴∠β=∠γ+∠α,
同理可得,当点P在AN上运动时,∠α=∠γ+∠β.


科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得:a= ,b= ;
)2,用含m、n的式子分别表示a、b,得:a= ,b= ;
(2)利用探索的结论,找一组正整数a、b、m、n (a、b都不超过20)
填空: + ![]() =( +
=( + ![]() )2;
)2;
(3)若a+6![]() =(m+n
=(m+n![]() )2,且a、m、n均为正整数,求a的值?
)2,且a、m、n均为正整数,求a的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校住校生宿舍有大小两种寝室若干间,据统计该校高一年级男生740人,使用了55间大寝室和50间小寝室,正好住满;女生730人,使用了大寝室50间和小寝室55间,也正好住满.求该校的大小寝室每间各住多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证△BED≌△CFD.
(2)已知EC=6,AC=10,求BE.
(3)当∠C=45°时,判断△DFC的周长与线段AC长度的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.
(1)求证:四边形ABCF是矩形;
(2)若ED=EC,求证:EA=EG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
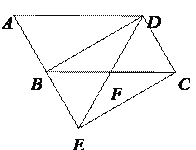
(1)求证:△BEF≌△CDF.
(2)连接BD,CE,若∠BFD=2∠A,求证四边形BECD是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com