
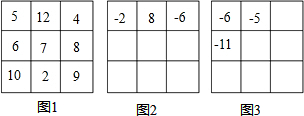
分析 (1)图2,先由第一行求出三阶幻方的幻和=-2+8-6=0,然后根据三阶幻方的幻和=中心数字×3,可求中心数字为0,然后再根据每个横行、每个竖列和每条对角线上的三个数之和都等于0,即可求出其它5个数;
(2)图3,先根据广义的三阶幻方,两红线的6个数之和=两蓝线的6个数字之和.(其中x算了两次)求出x的值;然后再根据三阶幻方的幻和=中心数字×3 (幻和就是每行或每列,或对角线上三个数字的和)可得:(-6)+B+(-8)=3B,即可求B的值,然后根据幻和即可求A、C、D、E的值.
解答 解:(1)图1,幻和=-2+8-6=0,
∵三阶幻方的幻和=中心数字×3,
∴中心数字为0,
∴对角线右下角的数字为:0-(-2)-0=2,
对角线左下角的数字为:0-(-6)-0=6,
中心数字的下方的数字为:0-8-0=-8,
中心数字的左边的数字为:0-(-2)-6=-4,
中心数字的右边的数字为:0-(-6)-2=4.
故填表如下: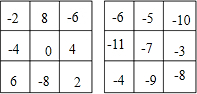
(2)分析如图所示: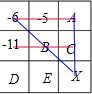
设其余6个位置的数字分别为:A,B,C,D,E,X,
①根据广义的三阶幻方,两红线的6个数之和=两蓝线的6个数字之和,可得:
[(-6)+(-5)+A]+[(-11)+B+C]=[(-6)+B+x]+(A+C+x),
(-6)+(-5)+(-11)+A+B+C=(-6)+A+B+C+2x,
(-6)+(-5)+(-11)=(-6)+2x,
(-5)+(-11)=2x,
2x=(-5)+(-11),
2x=-16,
x=-8,
②三阶幻方的幻和=中心数字×3,可得:
(-6)+B+(-8)=3B,
2B=(-6)+(-8),
B=-7,
③三阶幻方的幻和=中心数字×3,可得:
(-11)+(-7)+C=3×(-7),
-18+C=-21,
C=-3,
④同理,可得:
(-5)+(-7)+E=3×(-7),
-12+E=-21,
E=-9,
⑤同理,可得:
(-6)+(-5)+A=3×(-7),
-11+A=-21,
A=-10,
⑥同理,可得:
D+(-9)+(-8)=3×(-7),
D+(-17)=-21,
D=-4.
所以6个数字分别为:A=-10,B=-7,C=-3,D=-4,E=-9,X=-8.
点评 本题考查了有理数的加法,广义的三阶幻方,解题的关键是先确定中心数字,然后确定幻和.


科目:初中数学 来源: 题型:解答题
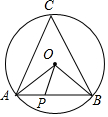 如图,⊙O的半径OA=2cm,弦AB=2$\sqrt{3}$cm,点C在圆上,点P为弦AB上一动点,求点P到圆心O的最短距离及∠C的度数.
如图,⊙O的半径OA=2cm,弦AB=2$\sqrt{3}$cm,点C在圆上,点P为弦AB上一动点,求点P到圆心O的最短距离及∠C的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
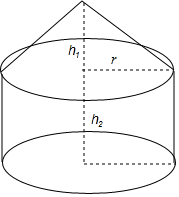 蒙古包可以近似地看作由圆锥和圆柱组成.如图,是一个蒙古包的示意图,现在想用毛毡搭建20个底面积为4πm2,高为3.5m,外围高为2m的蒙古包,至少需要多少平方米的毛毡?
蒙古包可以近似地看作由圆锥和圆柱组成.如图,是一个蒙古包的示意图,现在想用毛毡搭建20个底面积为4πm2,高为3.5m,外围高为2m的蒙古包,至少需要多少平方米的毛毡?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
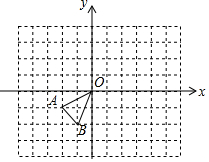 如图所示:
如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
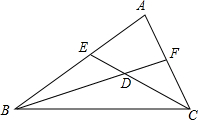 如图,在△ABC中,BF与CE交于点D,若BF和CE分别平分∠ABC和∠ACB.
如图,在△ABC中,BF与CE交于点D,若BF和CE分别平分∠ABC和∠ACB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com