
【题目】如图是抛物线![]() 的部分图象,其顶点坐标是
的部分图象,其顶点坐标是![]() ,给出下列结论:①
,给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
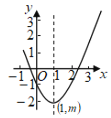
A.2B.3C.4D.5
科目:初中数学 来源: 题型:
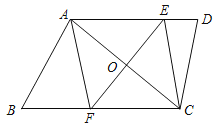
【题目】如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连结AF、CE.
(1)求证:△AOE≌△COF.
(2)试判断四边形AFCE的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x,y轴的交点分别为A,B,P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0,②x=3是ax2+bx+3=0的一个根,③△PAB周长的最小值是![]() +3
+3![]() .其中正确的是( )
.其中正确的是( )

A. ①②③ B. 仅有①② C. 仅有①③ D. 仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
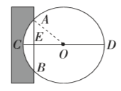
“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题:今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?用现在的数学语言表达是:如图,![]() 为
为![]() 的直径,弦
的直径,弦![]() ,垂足为
,垂足为![]() ,
,![]() 寸,
寸,![]() 尺,其中1尺
尺,其中1尺![]() 寸,求出直径
寸,求出直径![]() 的长.
的长.
解题过程如下:
连接![]() ,设
,设![]() 寸,则
寸,则![]() 寸.
寸.
∵![]() 尺,∴
尺,∴![]() 寸.
寸.
在![]() 中,
中,![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() 寸.
寸.
任务:
(1)上述解题过程运用了 定理和 定理.
(2)若原题改为已知![]() 寸,
寸,![]() 尺,请根据上述解题思路,求直径
尺,请根据上述解题思路,求直径![]() 的长.
的长.
(3)若继续往下锯,当锯到![]() 时,弦
时,弦![]() 所对圆周角的度数为 .
所对圆周角的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产![]() ,
,![]() 两种产品共10件,其生产成本和利润如下表.
两种产品共10件,其生产成本和利润如下表.
|
| |
成本(万元 | 2 | 5 |
利润(万元 | 1 | 3 |
(1)若工厂计划获利14万元,问![]() ,
,![]() 两种产品应分别生产多少件?
两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于22万元,问工厂有哪几种生产方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13,BC=15,CA=14,则tan∠EDF的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
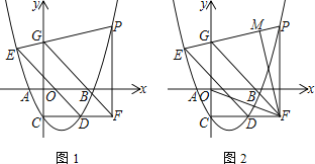
【题目】如图1,抛物线y=ax2-3ax-2交x轴于A、B(A左B右)两点,交y轴于点C,过C作CD∥x轴,交抛物线于点D,E(-2,3)在抛物线上.
(1)求抛物线的解析式;
(2)P为第一象限抛物线上一点,过点P作PF⊥CD,垂足为F,连接PE交y轴于G,求证:FG∥DE;
(3)如图2,在(2)的条件下,过点F作FM⊥PE于M.若∠OFM=45°,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,O是边AC上的点,以OC为半径的圆分别交边BC、AC于点D、E,过点D作DF⊥AB于点F.
(1)求证:直线DF是⊙O的切线;
(2)若OC=1,∠A=45°,求劣弧DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y4x4与x轴,y轴分别交于点A,B,点A在抛物线yax2bx3a(a0)上,将点B向右平移3个单位长度,得到点C.
(1)抛物线的顶点坐标为 (用含a的代数式表示)
(2)若a1,当t-1≤x≤t时,函数yax2bx3a(a0)的最大值为y1,最小值为y2,且y1y22,求t的值;
(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com