
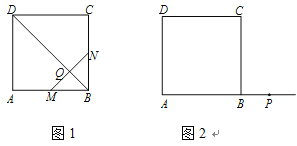
【题目】在正方形 ABCD 中,点 P 在射线 AB 上,连结 PC,PD,M,N 分别为 AB,PC 中点,连结 MN 交 PD 于点 Q.
(1)如图 1,当点 P 与点 B 重合时,求∠QMB 的度数;
(2)当点 P 在线段 AB 的延长线上时.
①依题意补全图2
②小聪通过观察、实验、提出猜想:在点P运动过程中,始终有QP=QM.小聪把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1延长BA到点 E,使AE=PB .要证QP=QM,只需证△PDA≌△ECB.
想法2:取PD 中点E ,连结NE,EA. 要证QP=QM只需证四边形NEAM 是平行四边形.
想 法3:过N 作 NE∥CB 交PB 于点 E ,要证QP=QM ,只要证明△NEM∽△DAP.
……
请你参考上面的想法,帮助小聪证明QP=QM. (一种方法即可)
【答案】(1)∠QMB 的度数为45°;
(2)①补全图2见解析;②证明见解析.
【解析】试题分析:(1)连接AC,由MN分别是AB、BC的中点可得,MN是![]() 的中位线,即可得到∠QMB 的度数为45°;(2)①根据题意画出图形;②根据每种方法提示解题即可;
的中位线,即可得到∠QMB 的度数为45°;(2)①根据题意画出图形;②根据每种方法提示解题即可;
试题解析:
(1) 连结AC,如图所示:
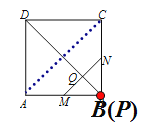
∵四边形ABCD是正方形
∴∠D AB=90°
∴∠C AB=45°
点 M,N 是 AB,BC 中点
∴MN∥AC
∴∠NMB=∠C AB=45°
∴∠QMB=∠C AB=45°
(2)① 如图所示:
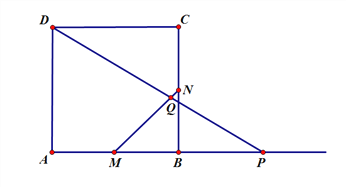
②想法1:延长BA 到点E,使AE=PB
∴BE=AP
∵正方形ABCD
∴∠PAD=∠EBC=90° AD=BC
∴△PDA≌△ECB
∠DPA=∠E
又点M 是AB 中点,AM=MB, 又AE=BP
∴AM+EA=MB+BP
∴EM=MP
∴M是EP中点
∴MN是△EPC的中位线
∴MN∥EC
∴∠E=∠NMP
∴∠NMP=∠DPA即∠QMP=∠QPM
∴QM=QP
想法2:取PD 中点E,连结NE,EA
∵E,N分别是PD,PC
∴EN∥CD,EN=![]() CD
CD
又CD∥AB,CD=AB
∴EN∥AB且EN=![]() AB
AB
∴EN=AM
∴四边形是NEAM是平行四边形
∴EA∥MN
∴∠EAB=∠NMB
又点E 是Rt△DAP 斜边DP中点
∴AE=EP
∴∠EAB=∠EPA
∴∠NMB=∠EPA
∴QM=QP
想法3:过N 作 NE∥CB 交PB 于点 E ,
∵CB⊥AB,
∴NE⊥AP
又∵N 是 PC中点
∴NE 是△CBP的中位线
∴NE=![]() BC
BC
又点E是B P中点
∴BE=![]() BP,MB=
BP,MB=![]() AB
AB
∴ME=![]() AP
AP
∴![]()
∠NEM=∠DAP=90°
∴△NEM∽△DAP
∴∠EMN=∠APD
∴QM=QP


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】某车间有34名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮和3个小齿轮配成一套,问分别安排多少名工人加工大小齿轮,才能刚好配套?若设加工大齿轮的工人有x名,则可列方程为( )
A. 3×10x=2×16(34﹣x) B. 3×16x=2×10(34﹣x)
C. 2×16x=3×10(34﹣x) D. 2×10x=3×16(34﹣x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.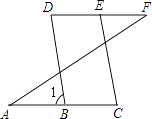
证明:∵∠A=∠F(已知)
∴AC∥()
∴∠D=∠1()
又∵∠C=∠D(已知)
∴∠1=()
∴BD∥CE()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com