
【题目】如图,等腰△ABC中,BA=BC,AO⊥BC于点O,AO=3CO=6.F是AB边上的一个动点,过F作FE∥BC交AC边于点E,交AO于点G,连结FO,EO,设EF长为x,△EFO的面积为S.
(1)求OB的长;
(2)求S关于x的函数表达式和x的取值范围;
(3)判断:当△EFO的面积最大时,△EFO和△CBA是否相似并说明理由.

【答案】(1)8;(2) ![]() (0<x<10) ;(3)见解析.
(0<x<10) ;(3)见解析.
【解析】
(1)由AO=3CO=6易得CO=2,结合AB=BC可得AB=BC=BO+2,这样在Rt△ABO中由AB2=AO2+BO2可得(2+OB)2=62+OB2,由此即可解得OB的值;
(2)由EF∥BC可得△AFE∽△ABC,由此可得![]() ,结合AG=AO-GO,EF=x及(1)中所得结论即可用含x的式子表达GO的长,再利用S△OEF=
,结合AG=AO-GO,EF=x及(1)中所得结论即可用含x的式子表达GO的长,再利用S△OEF=![]() EF·GO即可求得所求函数关系式了;
EF·GO即可求得所求函数关系式了;
(3)由(2)中所得解析配方可求得当△OEF面积最大时,EF=5,由此可知此时EF:BC=1:2,由EF∥BC可得△AFE∽△ABC,从而可得![]() ,由此可得点E、F是AC、AB的中点,结合AO⊥BC可得OF=
,由此可得点E、F是AC、AB的中点,结合AO⊥BC可得OF=![]() AB,OE=
AB,OE=![]() AC,从而可得
AC,从而可得![]() ,由此即可得到△EFO∽△CBA.
,由此即可得到△EFO∽△CBA.
(1)∵AO=3CO=6,
∴CO=2,
∴AB =BC= BO+2,
∵AO⊥BC,
∴AB2=AO2+OB2,
∴(2+OB)2=36+OB2,
解得OB=8;
(2) 由(1)得BC=OB+2=10,
∵FE∥BC,
∴△AFE∽△ABC,
∴![]() ,即
,即 ![]() ,
,
解得:OG=![]() ,
,
∴S=![]() EF×OG=
EF×OG=![]() ,
,
即![]() (0<x<10) ;
(0<x<10) ;
(3) 当△EFO的面积最大时,△EFO∽△CBA,理由如下:
∵![]()
![]() ,
,
∴当x=5,即EF=5时,S最大=![]() ,
,
此时:![]() ,
,
∵FE∥BC,
∴△AFE∽△ABC,
∴![]() ,
,
∴E,F分别是AC,AB的中点,
∵AO⊥BC,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴△EFO∽△CBA.


科目:初中数学 来源: 题型:
【题目】如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ).

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知三角形纸片![]() ,将纸片折叠,使点
,将纸片折叠,使点![]() 与点
与点![]() 重合,折痕分别与边
重合,折痕分别与边![]() 交于点
交于点![]() .
.
(1)画出直线![]() ;
;
(2)若点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,请画出点
,请画出点![]() ;
;
(3)在(2)的条件下,联结![]() ,如果
,如果![]() 的面积为2,
的面积为2,![]() 的面积为
的面积为![]() ,那么
,那么![]() 的面积等于 .
的面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】银杏树具有观赏、经济、药用等价值而深受人们喜爱.在银杏种植基地有![]() 、
、![]() 两个品种的树苗出售,已知
两个品种的树苗出售,已知![]() 种比
种比![]() 种每株多20元,买1株
种每株多20元,买1株![]() 种树苗和2株
种树苗和2株![]() 种树苗共需200元.
种树苗共需200元.
(1)问![]() 、
、![]() 两种树苗每株分别多少元?
两种树苗每株分别多少元?
(2)为扩大种植,某农户准备购买![]() 、
、![]() 两种银杏树苗共36株,且
两种银杏树苗共36株,且![]() 种树苗数量不少于
种树苗数量不少于![]() 种数量的一半,请求出费用最省的购买方案.
种数量的一半,请求出费用最省的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果绘制成了如图的统计图.在这20位同学中,本学期购买课外书的花费的众数和中位数分别是( )

A. 50,50 B. 50,30 C. 80,50 D. 30,50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量山坡上一棵树PQ的高度,小明在点A处利用测角仪测得树顶P的仰角为450 ,然后他沿着正对树PQ的方向前进10m到达B点处,此时测得树顶P和树底Q的仰角分别是600和300,设PQ垂直于AB,且垂足为C.
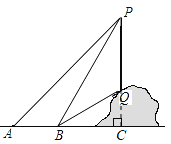
(1)求∠BPQ的度数;
(2)求树PQ的高度(结果精确到0.1m, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com