
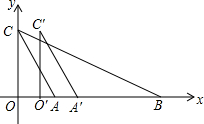
 如图,△ABC中,A(1,0),B(4,0),C(0,2),将△AOC沿x轴的正半轴以每秒1个单位的速度向右平移得到△A′O′C′,设运动时间为t(s),△A′O′C′与△ABC重叠部分的面积为s,求s与t的函数关系式,并说明自变量t的取值范围.
如图,△ABC中,A(1,0),B(4,0),C(0,2),将△AOC沿x轴的正半轴以每秒1个单位的速度向右平移得到△A′O′C′,设运动时间为t(s),△A′O′C′与△ABC重叠部分的面积为s,求s与t的函数关系式,并说明自变量t的取值范围. 分析 分三种情形:①0<t≤1②1<t≤4③t>4求出s与t的关系,图1中,利用s=S△BO′F-S△AO′H-S△BA′D即可解答,图2中利用s=S△BO′F-S△BA′D即可求解,图3中利用S=S△BO′F=$\frac{1}{2}$BO′•O′F求解.
解答 解:过D作DE⊥BO于E,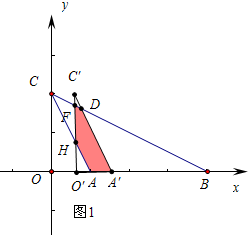
∵A(1,0),B(4,0),C(0,2),
∴OA=1,OB=4,OC=2,
①当0<t≤1时,如图1,∵AC∥A′C′,
∴△A′BD∽△ABC,
∴$\frac{A′B}{AB}=\frac{DE}{OC}$,
∴$\frac{4-1-t}{3}$=$\frac{DE}{2}$,
∴DE=$\frac{6-2t}{3}$,
∵OC∥OC′,
∴△BFO′∽△BCO,
∴$\frac{O′F}{OC}$=$\frac{O′B}{OB}$,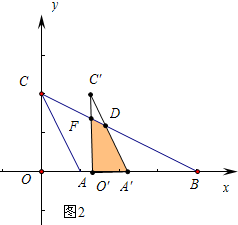
∴$\frac{O′F}{2}$=$\frac{4-t}{4}$,
∴O′F=$\frac{4-t}{2}$,
∵HO′∥CO,
∴$\frac{HO′}{CO}=\frac{AO′}{AO}$,
∴$\frac{HO′}{2}=\frac{1-t}{1}$,
∴HO′=2(1-t),
∴s=S△BO′F-S△AO′H-S△BA′D=$\frac{1}{2}$(4-t)•$\frac{4-t}{2}$-$\frac{1}{2}$×(4-t-1)•$\frac{6-2t}{3}$-$\frac{1}{2}(1-t)•2(1-t)$=-$\frac{13}{12}{t}^{2}+2t$,
②当1<t≤4时,如图2,
s=S△BO′F-S△BA′D=$\frac{1}{2}$(4-t)•$\frac{4-t}{2}$-$\frac{1}{2}$×(4-t-1)•$\frac{6-2t}{3}$=-$\frac{1}{12}{t}^{2}$+1,
③t>4时,如图3,
S=S△BO′F=$\frac{1}{2}$BO′•O′F=$\frac{1}{2}$(4-t)•$\frac{4-t}{2}$=$\frac{1}{4}$t2-2t+4,
综上所述:S=$\left\{\begin{array}{l}{-\frac{13}{12}{t}^{2}+2t}&{(0<t≤1)}\\{-\frac{1}{12}{t}^{2}+1}&{(1<t≤4)}\\{\frac{1}{4}{t}^{2}-2t+4}&{(t>4)}\end{array}\right.$.
点评 本题考查了动点问题的函数图象,相似三角形的判定和性质,平移的性质.三角形的面积,学会分类讨论、正确画出图象是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等腰直角△ABC中,AC=BC,AD⊥AB(点D在AB的右上方),E为AB边上一点,且BE=4,DE=6,当CD平分∠ADE时,CE的长度为2$\sqrt{6}$.
如图,在等腰直角△ABC中,AC=BC,AD⊥AB(点D在AB的右上方),E为AB边上一点,且BE=4,DE=6,当CD平分∠ADE时,CE的长度为2$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC和△ADE中,AB=AC,∠ADE=∠AED,∠BAC+∠EAD=180°,BE,CD,F为BE的中点,连接AF,当∠BAE=90°时,求证:CD=2AF.
如图,在△ABC和△ADE中,AB=AC,∠ADE=∠AED,∠BAC+∠EAD=180°,BE,CD,F为BE的中点,连接AF,当∠BAE=90°时,求证:CD=2AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com