练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．下列四组线段中，能构成直角三角形的是（　　）
    A．9，12，13B．$\frac{1}{3}$，$\frac{1}{4}$，$\frac{1}{5}$C．32，42，52D．1，$\sqrt{2}$，$\sqrt{3}$

    分析 利用勾股定理的逆定理证明三角形是直角三角形，需验证两小边的平方和是否等于最长边的平方．

    解答 解：A、∵92+122≠132，∴不能构成直角三角形，故选项不符合题意；
    B、∵（$\frac{1}{4}$）2+（$\frac{1}{4}$）2=（$\frac{1}{3}$）2，∴不能构成直角三角形，故选项不符合题意；
    C、∵（32）2+（42）2≠（52）2，∴不能构成直角三角形，故选项不符合题意；
    D、∵12+（$\sqrt{2}$）2=（$\sqrt{3}$）2，∴能构成直角三角形，故选项符合题意．
    故选D．

    点评 此题主要考查了勾股数，关键是掌握勾股数的定义，及勾股定理的逆定理：已知△ABC的三边满足a2+b2=c2，则△ABC是直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．已知两个完全相同的直角三角形纸片△ABC、△DEF，如图放置，点B、D重合，点F在BC上，AB与EF交于点G．∠C=∠EFB=90°，∠E=∠ABC=30°，现将图中的△ABC绕点F按每秒10°的速度沿逆时针方向旋转180°，在旋转的过程中，△ABC恰有一边与DE平行的时间为3或12或15s．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．阅读下列材料：
    问题：已知方程x2+x-1=0，求一个一元二次方程，使它的根分别是已知方程根的2倍．
    解：设所求方程的根为y，则y=2x，所以x=$\frac{y}{2}$，把x=$\frac{y}{2}$，代入已知方程，得（$\frac{y}{2}$）2+$\frac{y}{2}$-1=0．
    化简，得y2+2y-4=0，
    故所求方程为y2+2y-4=0
    这种利用方程根的代换求新方程的方法，我们称为“换根法”．
    请用阅读材料提供的“换根法”求新方程（要求：把所求方程化为一般形式）：
    （1）已知方程x2+2x-1=0，求一个一元二次方程，使它的根分别是已知方程根的相反数，则所求方程为y2-2y-1=0；
    （2）已知关于x的一元二次方程ax2+bx+c=0（a≠0）有两个不等于零的实数根，求一个一元二次方程，使它的根分别是已知方程根的倒数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，在Rt△ABC中，∠C=90°，∠A=60°，AB=12cm，若点P从点B出发以2cm/s的速度向点A运动，点Q从点A出发以1cm/s的速度向点C运动，设P、Q分别从点B、A同时出发，运动的时间为ts．
    （1）用含t的式子表示线段AP、AQ的长；
    （2）当t为何值时，△APQ是以PQ为底边的等腰三角形？
    （3）当t为何值时，PQ∥BC？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

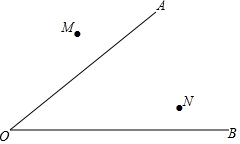    8．2016年6月10日，我海军两艘军舰“温州526舰”、“马鞍山525舰”在我钓鱼岛海域进行巡航．如图，两舰约定在点P会合，已知P点到M、N两地的距离相等，且到OA、OB两条航线的距离相等，请在下图中找出P点的位置．（保留作图痕迹，不写作法）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列说法中，正确的是（　　）
    A．1的平方根是1B．-1是1的平方根C．8的立方根是±2D．$\sqrt{9}$=±3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：$\sqrt{2\frac{1}{4}}$+$\root{3}{-64}$×$\frac{1}{4}$-（-$\sqrt{\frac{1}{2}}$）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．化简$\frac{{{x^2}-1}}{x-1}$正确的是（　　）
    A．$\frac{{{x^2}-1}}{x-1}=\frac{{{{（x-1）}^2}}}{x-1}=\frac{1}{x-1}$B．$\frac{{{x^2}-1}}{x-1}=\frac{{{{（x-1）}^2}}}{x-1}=x-1$
    C．$\frac{{{x^2}-1}}{x-1}=\frac{（x+1）（x-1）}{x-1}=x+1$D．$\frac{{{x^2}-1}}{x-1}=\frac{（x+1）（x-1）}{x-1}=\frac{1}{x+1}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，在△ABC中，∠A=m°，∠ABC和∠ACD的三等分线交于点P、Q，求∠P+∠Q．（用含m的式子表示）

    查看答案和解析>>

    同步练习册答案