
【题目】在ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF. 
(1)求证:四边形BFDE是矩形.
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的角平分线.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵CF=AE,
∴BE=DF.
∴四边形BFDE为平行四边形.
∵DE⊥AB,
∴∠DEB=90°.
∴四边形BFDE是矩形
(2)证明:由(1)得,四边形BFDE是矩形,
∴∠BFD=90°.
∴∠BFC=90°,
在Rt△BFC中,由勾股定理得:BC= ![]() =
= ![]() =10.
=10.
∴AD=BC=10.
∵DF=10,
∴AD=DF.
∴∠DAF=∠DFA.
∵AB∥CD,
∴∠DFA=∠FAB.
∴∠DAF=∠FAB.
∴AF平分∠DAB.
即AF是∠DAB的平分线
【解析】(1)由平行四边形的性质和已知条件得出BE=DF,证明四边形BFDE为平行四边形,再由DE⊥AB,即可得出结论;(2)由矩形的性质和勾股定理求出BC,得出AD=BC=DF,证出∠DAF=∠DFA,再由平行线的性质即可得出结论.
【考点精析】通过灵活运用平行四边形的性质和矩形的判定方法,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形即可以解答此题.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC>AC , 点D在BC上,且DC=AC , ∠ACB的平分线CF交AD于F , 点E是AB的中点,连接EF . 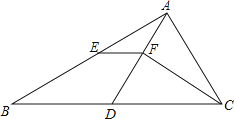
(1)求证:2EF=BD ,
(2)四边形BDFE的面积为6,求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).
(1)点( ![]() ,
, ![]() )的“双角坐标”为;
)的“双角坐标”为;
(2)若点P到x轴的距离为 ![]() ,则m+n的最小值为 .
,则m+n的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究函数y=x+ ![]() 的图象与性质
的图象与性质
(1)函数y=x+ ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下列四个函数图象中,函数y=x+ ![]() 的图象大致是
的图象大致是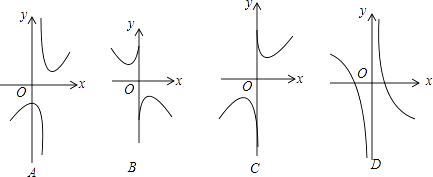
(3)对于函数y=x+ ![]() ,求当x>0时,y的取值范围.
,求当x>0时,y的取值范围.
请将下面求解此问题的过程补充完整:
解:∵x>0
∴y=x+ ![]()
=( ![]() )2+(
)2+( ![]() )2
)2
=( ![]() ﹣
﹣ ![]() )2+
)2+
∵( ![]() ﹣
﹣ ![]() )2≥0,
)2≥0,
∴y .
(4)若函数y= ![]() ,则y的取值范围是
,则y的取值范围是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,∠A=30°,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连结BD,DE. 则∠BDE的度数为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y1=mx2+(m﹣3)x﹣3(m>0)与x轴交于A、B两点,且点A在点B的左侧,与y轴交于点C,OB=OC. 
(1)求这条抛物线的表达式;
(2)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,若点C在直线y2=﹣3x+t上,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数 ![]() 与反比例函数
与反比例函数 ![]() 的图象在第一象限的交点为A(1,n).
的图象在第一象限的交点为A(1,n). 
(1)求m与n的值;
(2)设一次函数的图象与x轴交于点B,连结OA,求∠BAO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳影子定位技术是通过分析视频中物体的太阳影子变化,确定视频拍摄地点的一种方法.为了确定视频拍摄地的经度,我们需要对比视频中影子最短的时刻与同一天东经120度影子最短的时刻.在一定条件下,直杆的太阳影子长度l(单位:米)与时刻t(单位:时)的关系满足函数关系l=at2+bt+c(a,b,c是常数),如图记录了三个时刻的数据,根据上述函数模型和记录的数据,则该地影子最短时,最接近的时刻t是( ) 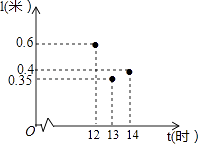
A.12.75
B.13
C.13.33
D.13.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x≤100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
“文明在我身边”摄影比赛成绩统计表
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x≤100 | b | 0.06 |
合计 | 1 |
根据以上信息解答下列问题:
(1)统计表中c的值为;样本成绩的中位数落在分数段中;
(2)补全频数分布直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评作品数量是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com