
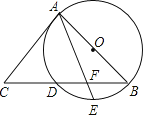
����Ŀ�����ǰ�һ����Բ�������ߵ�һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣬��ô����ֱ�߽�������Բ�������ߣ���ͼ��ʾ����A��B��C��D�ֱ��ǡ���Բ����������Ľ��㣬��֪��D������Ϊ��0��-3����ABΪ��Բ��ֱ������ԲԲ��M������Ϊ��1��0������Բ�뾶Ϊ2��

��1�������������Բ�������߲��ֵĽ���ʽ����д���Ա�����ȡֵ��Χ��
��2���������������C�ġ���Բ�����ߵĽ���ʽ�����Կ���
��3�������Խ���һ�룬�����������������D�ġ���Բ�����ߵĽ���ʽ��
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ����3��
����3��![]() .
.
��������
��1����֪��![]() �������ʽΪ����ʽ��
�������ʽΪ����ʽ��![]() ������D���������⼴�ɣ�
������D���������⼴�ɣ�
��2���辭����C�ġ���Բ������CE��x���ڵ�E������CM����![]() �У��ɹ��ɶ�����֪OC������֪��C���꣬��ֱ�������οɵ�
�У��ɹ��ɶ�����֪OC������֪��C���꣬��ֱ�������οɵ�![]() ����
����![]() �У���ֱ�������οɵ�EM������֪��E���꣬��ֱ��CE�Ľ���ʽΪ
�У���ֱ�������οɵ�EM������֪��E���꣬��ֱ��CE�Ľ���ʽΪ![]() ������
������![]() ��
��![]() ��������⼴�ɣ�
��������⼴�ɣ�
��3�������![]() �ġ���Բ�����ߵĽ���ʽΪ
�ġ���Բ�����ߵĽ���ʽΪ![]() ���������֪����
���������֪����![]() ��������ȵ�ʵ����������
��������ȵ�ʵ����������![]() �ɵ�mֵ.
�ɵ�mֵ.
�⣺��1����ABΪ��Բ��ֱ������ԲԲ��M������Ϊ��1��0������Բ�뾶Ϊ2��֪![]() ��
��
�衰��Բ�������߲��ֵĽ���ʽΪ![]() ��
��
����![]() ����
����![]() ��
��![]() ��
��
���![]() ��
��
![]()
���ԡ���Բ�������߲��ֵĽ���ʽΪ![]() ���Ա�����ȡֵ��ΧΪ
���Ա�����ȡֵ��ΧΪ![]() ��
��
��2���辭����C�ġ���Բ������CE��x���ڵ�E������CM��

��![]() ��
�У�![]() �����ݹ��ɶ�����
�����ݹ��ɶ�����![]() ����
����![]() ��
��
![]()
![]()
��![]() ��
�У�![]()
![]()
![]()
![]()
��ֱ��CE�Ľ���ʽΪ![]() ��
��
����![]() ��
��![]() �����
�����
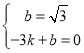
���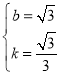
���Ծ�����C�ġ���Բ�����ߵĽ���ʽ![]() ��
��
��3�������![]() ������Բ�����ߵĽ���ʽΪ
������Բ�����ߵĽ���ʽΪ![]() ��
��
�������֪������![]() ֻ��һ��⣬
ֻ��һ��⣬
��![]() ��������ȵ�ʵ������
��������ȵ�ʵ������
�����![]()
![]()
���![]() ��
��![]() ����ȥ��
����ȥ��
���Ծ�����D������Բ�����ߵĽ���ʽΪ![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
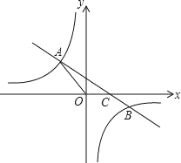
����Ŀ����ͼ��һ�κ���y��kx+b��k��0����ͼ���뷴��������![]() ��ͼ���ڶ����������ڵ�A��B���㣬��x�ύ��C�㣬��A������Ϊ����2��3������B������Ϊ��4��n����
��ͼ���ڶ����������ڵ�A��B���㣬��x�ύ��C�㣬��A������Ϊ����2��3������B������Ϊ��4��n����
��1����÷�����������һ�κ����Ľ���ʽ��
��2����x�����Ƿ���ڵ�P��ʹ��APC��ֱ�������Σ����棬�����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y����x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C����OΪ����ԭ�㣬��E���������ϣ���F��x���ϣ��ı���OCEFΪ���Σ���OF��2��EF��3����DΪֱ��AE�Ϸ��������ϵ�һ��
��1��������������Ӧ�ĺ�������ʽ��
��2�����ADE��������ֵ�ʹ�ʱ��D�����ꣻ
��3������AOC�Ƶ�C��ʱ����ת90������A��Ӧ��Ϊ��G���ʵ�G�Ƿ��ڸ��������ϣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
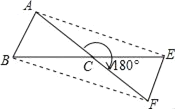
����Ŀ������ABC�Ƶ�C��ת180��õ���FEC��
��1���Բ���AE��BF�кι�ϵ��˵�����ɣ�
��2������ABC�����Ϊ3cm2�����ı���ABFE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������м���ԭ��360ǧ�ˣ�����ԭ��290ǧ�ˣ��ƻ�����������ԭ������A��B���ֲ�Ʒ��50������֪����һ��A�ֲ�Ʒ�ü���ԭ��9ǧ�ˣ�����ԭ��3ǧ�ˣ��ɻ���700Ԫ������һ��B�ֲ�Ʒ�ü���ԭ��4ǧ�ˣ�����ԭ��10ǧ�ˣ��ɻ���1200Ԫ��
��1����Ҫ����A��B���ֲ�Ʒ���������������ļ��ַ�����������Ƴ�����
��2��������A��B���ֲ�Ʒ������ΪyԪ������һ�ֲ�Ʒ��������Ϊx������д��y��x֮��ĺ�����ϵʽ�������ú���������˵�����ַ������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ���� BC����O�ڵ�D��E��![]() ���е㣬����AE��BC�ڵ�F����ACB =2��EAB��
���е㣬����AE��BC�ڵ�F����ACB =2��EAB��
��1����֤��AC�ǡ�O�����ߣ�
��2����![]() ��
��![]() ����BF�ij���
����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ȫУѧ����ѧ�Ľ�ͨ��ʽ����У���꼶��8�����4��ͬѧ���������һ�ݵ����ʾ����Ը�У����ѧ��������������飮��A�������г�����B���˹���������C�����У���D����˽�ҳ�����E��������ʽ�� ����ѡ�Ҫ����ͬѧ���е�ѡ���������������Ƴ�����ͳ��ͼ1������ͳ��ͼ2������������Ϣ�� ����������⣺

��1�����ν��ܵ������������ �ˣ� ��������ͳ��ͼ����������
��2��������ͳ��ͼ�У�����������������ռ�İٷֱ��� ����������ʽ���������ε�Բ�ĽǶ����� ��
��3����֪��4��ͬѧ����2��Ůͬѧ��Ҫ����ѡ����ͬѧ�㱨���������������б�������״ͼ�ķ����� ���ǡ��ѡ��1��������1��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��0����ͬһֱ������ϵ�У�����y=ax��y=ax2��ͼ���п����ǣ�������
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B��90����BC��AB����BC����ȡ��D��ʹAB��BD������������ABDE��DE��AC�ڵ�F����EG��AC��AC�ڵ�G����BC�ڵ�H��
��1����֤��EF��DH��
��2����AB��6��DH��2DF����AC�ij���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com