
分析 连接AO,交BC于点E,连接BO,求出$\widehat{AB}$=$\widehat{AC}$,根据垂径定理得出OA⊥BC,BC=2BE,设AE=x,则BE=2x,OE=5-x,根据勾股定理得出方程(2x)2+(5-x)2=52,求出方程的解即可.
解答 解:连接AO,交BC于点E,连接BO,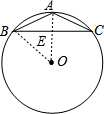
∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
又∵OA是半径,
∴OA⊥BC,BC=2BE,
在Rt△ABE中,∵tan∠ABC=$\frac{1}{2}$,
∴$\frac{AE}{BE}$=$\frac{1}{2}$,
设AE=x,则BE=2x,OE=5-x,
在Rt△EO中,BE2+OE2=OB2,
∴(2x)2+(5-x)2=52,
解得:x1=0(舍去),x2=2,
∴BE=2x=4,
∴BC=2BE=8.
点评 本题考查了圆心角、弧、弦之间的关系,垂径定理,解直角三角形,勾股定理的应用,解此题的关键是构造直角三角形,用了方程思想,难度适中.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ a2c | B. | $\frac{1}{4}$ ac | C. | $\frac{9}{4}$ a2c | D. | $\frac{9}{4}$ ac |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+3)2(x+2)(x-2) | B. | (x2-9)2(x2-4) | C. | (x2-9)2(x-4)2 | D. | (x+3)2(x-3)2(x2+2)(x-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com