
【题目】(探究与证明)
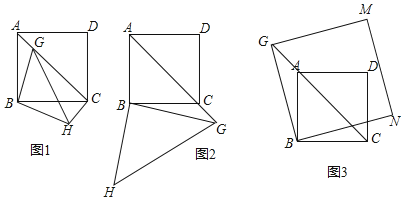
在正方形ABCD中,G是射线AC上一动点(不与点A、C重合),连BG,作BH⊥BG,且使BH=BG,连GH、CH.
(1)若G在AC上(如图1),则:①图中与△ABG全等的三角形是 .
②线段AG、CG、GH之间的数量关系是 .
(2)若G在AC的延长线上(如图2),那么线段AG、CG、BG之间有怎样的数量关系?写出结论并给出证明;
(应用)(3)如图3,G在正方形ABCD的对角线CA的延长线上,以BG为边作正方形BGMN,若AG=2,AD=4,请直接写出正方形BGMN的面积.
【答案】(1)①△CBH,②AG2+CG2=GH 2(2)20+8![]()
【解析】
探究与证明(1)①由题意可得AB=BC,BG=BH,∠ABG=∠CBH 可证△ABG≌△BCH
②由△ABG≌△BCH可得AG=CH,∠ACH=90° 可得AG、CG、GH之间的数量关系.
(2)连接CH,可证△ABG≌△BCH,可得△CHG是直角三角形,则AG2+CG2=GH2,且HG2=BG2+BH2=2BG2,可得线段AG、CG、BG之间.
应用:(3)连接BD交AC于O,由正方形ABCD可得AC⊥BD,AO=BO=CO=2![]() ,则根据正方形GBMN的面积=BG2=GO2+BO2.可求正方形GBMN的面积.
,则根据正方形GBMN的面积=BG2=GO2+BO2.可求正方形GBMN的面积.
解:探究与证明:(1)①△CBH,②AG2+CG2=GH 2
理由如下:
∵ABCD是正方形
∴AB=CB,∠ABC=90°,∠BAC=∠BCA=45°
又∵GB⊥BH
∴∠ABG=∠CBH且BG=BH,AB=BC
∴△ABG≌△BCH
∴∠BAC=∠BCH=45°,AG=CH
∴∠GCH=90°
在Rt△GCH中,CH2+CG2=GH 2
∴AG2+CG2=GH 2
(2)

如图2,连CH
∵四边形ABCD是正方形
∴∠ABC=90°,AB=BC
∵∠GBH=90°
∴∠ABC+∠GBC=∠GBH+∠GBC
即:∠ABG=∠CBH
又∵BH=BG
∴△ABG≌△CBH
∴AG=CH,∠BCH=∠BAC=45°
∴∠ACH=∠ACB+∠BCH=45°+45°=90°
∴AG⊥CH
∴CH2+CG2=GH 2
∴AG2+CG2=GH2
∵HG2=BG2+BH2=2BG2
∴AG2+CG2=2BG2
应用:(3)如图连接BD交AC于O
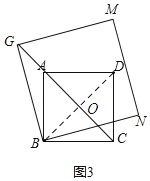
∵四边形ABCD 是正方形,AD=4,
∴AC=4![]() ,BO=AO=DO=CO=2
,BO=AO=DO=CO=2![]() ,AC⊥BD,
,AC⊥BD,
∴BG2=GO2+BO2,
∵S正方形GBNM=BG2=GO2+BO2=(2+2![]() )2/span>+(2
)2/span>+(2![]() )2=20+8
)2=20+8![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读与思考:利用多项式的乘法法则,可以得到![]() ,反过来,则有
,反过来,则有![]() 利用这个式子可以将某些二次项系数是1的二次三项式分解因式。例如:将式子
利用这个式子可以将某些二次项系数是1的二次三项式分解因式。例如:将式子![]() 分解因式.这个式子的常数项
分解因式.这个式子的常数项![]() ,一次项系数
,一次项系数![]() ,所以
,所以![]() .
.
解:![]() .
.
上述分解因式![]() 的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图).
的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图).

请仿照上面的方法,解答下列问题:
(1)分解因式:![]() ;
;
(2)分解因式:![]() ;
;
(3)若![]() 可分解为两个一次因式的积,写出整数P的所有可能值.
可分解为两个一次因式的积,写出整数P的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完“数据的收集、整理与描述”后,李明对本班期中考试数学成绩(成绩均为整数,满分为150分)作了统计分析(每个人的成绩各不相同,且最低分为50分),绘制成如下频数分布表和频数分布直方图(为避免分数出现在分组的端点处,李明将分点取小数),请你根据图表提供的信息,解答下列问题:
分组 | 频数 | 频率 |
49.5~69.5 | 2 | 0.04 |
69.5~89.5 | 8 |
|
89.5~109.5 | 20 | 0.40 |
109.5~129.5 |
| 0.32 |
129.5~150.5 | 4 | 0.08 |
合计 |
| 1 |
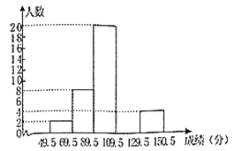
(1)分布表中![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)补全频数分布直方图;
(3)若画该班期中考试数学成绩的扇形统计图,则分数在89.5~109.5之间的扇形圆心角的度数是____![]() ;
;
(4)张亮同学成绩为109分,他说:“我们班上比我成绩高的人还有![]() ,我要继续努力.”他的说法正确吗?请说明理由.
,我要继续努力.”他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、②,在平面直角坐标系中,一边长为2的等边三角板CDE恰好与坐标系中的△OAB重合,现将三角板CDE绕边AB的中点G(G点也是DE的中点),按顺时针方向旋转180°到△C′ED的位置.

(1)求C′点的坐标;
(2)求经过O、A、C′三点的抛物线的解析式;
(3)如图③,⊙G是以AB为直径的圆,过B点作⊙G的切线与x轴相交于点F,求切线BF的解析式;
(4)在(3)的条件下,抛物线上是否存在一点M,使得△BOF与△AOM相似?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
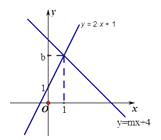
【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“寒假”期间,某校小记者随机调查了某地区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:
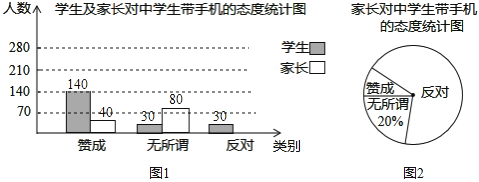
(1)求这次调查的家长人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)已知某地区共6500名家长,估计其中反对中学生带手机的大约有多少名家长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某个大型商场的自动扶梯侧面示意图,已知自动扶梯AC的坡度为1:2,AC的长度为5![]() 米,AB为底楼地面,CD为二楼侧面,EF为二楼楼顶,当然有EF∥AB∥CD,E为自动扶梯AC的最高端C的正上方,过C的直线EG⊥AB于G,在自动扶梯的底端A测得E的仰角为42°,求该商场二楼的楼高CE.
米,AB为底楼地面,CD为二楼侧面,EF为二楼楼顶,当然有EF∥AB∥CD,E为自动扶梯AC的最高端C的正上方,过C的直线EG⊥AB于G,在自动扶梯的底端A测得E的仰角为42°,求该商场二楼的楼高CE.
(参考数据:sin42°=![]() ,cos42°=
,cos42°=![]() ,tan42°=
,tan42°=![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级为庆祝中华人民共和国建国70周年,准备举行唱红歌、颂经典活动.八年级(2)班积极准备,需购买文件夹若干,某文具店有甲、乙两种文件夹.
(1)若该班只购买甲种文件夹,且购买甲种文件夹的花费![]() (单位:元)与其购买数量
(单位:元)与其购买数量![]() (单位:件)满足一次函数关系,若购买20个,需花费180元;若购买30个,需花费260元.该班若需购买甲种文件夹60件,求需花费多少元?
(单位:件)满足一次函数关系,若购买20个,需花费180元;若购买30个,需花费260元.该班若需购买甲种文件夹60件,求需花费多少元?
(2)若该班购买甲,乙两种文件夹,那么甲种文件夹的单价比乙种文件夹的单价贵2元,若用240元购买甲种文件夹的数量与用180元购买乙种文件夹的数量相同.求该文具店甲乙两种文件夹的单价分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两座建筑物AB及CD,其中A,C距离为60米,在AB的顶点B处测得CD的顶部D的仰角β=30°,测得其底部C的俯角α=45°,求两座建筑物AB及CD的高度(保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com