
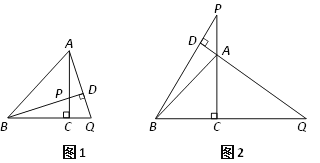
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
(1)如图1,当P在线段AC上时,请说明:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,⑴中的结论是否成立? (填“成立”或“不成立”)
【答案】(1)证明见解析;(2)成立.
【解析】试题分析:(1)首先根据内角和定理得出∠DAP=∠CBP,进而得出△ACQ≌△BCP即可得出答案;(2)延长BA交PQ于H,由于∠ACQ=∠BDQ=90°,∠AQC=∠BQD,得到∠CAQ=∠DBQ,推出△AQC≌△BPC(ASA)即可得出结论.
试题解析:(1)∵∠ACB=∠ADB=90°,∠APD=∠BPC,
∴∠DAP=∠CBP.
在△ACQ和△BCP中,

∴△ACQ ≌△BCP(ASA).
∴BP=AQ.
(2)成立,
理由:延长BA交PQ于H,
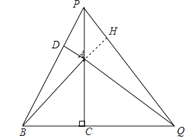
∵∠ACQ=∠BDQ=90°,∠AQC=∠BQD,
∴∠CAQ=∠DBQ,
在△AQC和△BPC中, 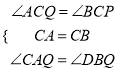
∴△AQC≌△BPC(ASA),
∴AQ=BP,
故答案为:成立;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列由左到右的变形,属于因式分解的是( )
A.(x+2)(x﹣2)=x2﹣4
B.x2﹣4=(x+2)(x﹣2)
C.x2﹣4+3x=(x+2)(x﹣2)+3x
D.x2+4=(x+2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a+b+c=0,则下列结论正确的是( )
A. a=b=c=0
B. a,b,c中至少有两个是负数
C. a,b,c中可以没有负数
D. a,b,c中至少有两个是正数
查看答案和解析>>
科目:初中数学 来源: 题型:
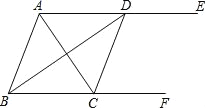
【题目】如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若AB=5,AC=6,求AE,BF之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com