
ЁОЬтФПЁПФГАрЁАЪ§бЇаЫШЄаЁзщЁБЖдКЏЪ§yЃН![]() +xЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЌЬНОПЙ§ГЬШчЯТЃЌЧыВЙГфЭъећЃЎ
+xЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЌЬНОПЙ§ГЬШчЯТЃЌЧыВЙГфЭъећЃЎ
(1)КЏЪ§yЃН![]() +xЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЛ
+xЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЛ
(2)ЯТБэЪЧyгыxЕФМИзщЖдгІжЕЃЎ
x | Ё | Љ3 | Љ2 | Љ1 | 0 |
|
|
|
| 2 | 3 | 4 | 5 | Ё |
y | Ё | Љ | Љ | Љ | Љ1 | Љ | Љ |
|
| 3 |
| m |
| Ё |
ЧѓmЕФжЕЃЛ
(3)ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіСЫвдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
(4)НјвЛВНЬНОПЗЂЯжЃЌИУКЏЪ§ЭМЯѓдкЕквЛЯѓЯоФкЕФзюЕЭЕуЕФзјБъЪЧ(2ЃЌ3)ЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌаДГіИУКЏЪ§ЕФЦфЫќаджЪ(вЛЬѕМДПЩ)ЃКЁЁ ЁЁЃЎ
(5)аЁУїЗЂЯжЃЌЂйИУКЏЪ§ЕФЭМЯѓЙигкЕу(ЁЁ ЁЁЃЌЁЁ ЁЁ)ГЩжааФЖдГЦЃЛ
ЂкИУКЏЪ§ЕФЭМЯѓгывЛЬѕДЙжБгкxжсЕФжБЯпЮоНЛЕуЃЌдђетЬѕжБЯпЮЊЁЁ ЁЁЃЛ
ЂлжБЯпyЃНmгыИУКЏЪ§ЕФЭМЯѓЮоНЛЕуЃЌдђmЕФШЁжЕЗЖЮЇЮЊЁЁ ЁЁЃЎ

ЁОД№АИЁП(1)xЁй1,(2)![]() ,(4)xЃО2ЪБyЫцxЕФдіДѓЖјдіДѓ,
,(4)xЃО2ЪБyЫцxЕФдіДѓЖјдіДѓ,
(5)Ђй( ![]() ЃЌ
ЃЌ![]() )ЃЌЂкx=1ЃЌЂлЉ1ЃМmЃМ3.
)ЃЌЂкx=1ЃЌЂлЉ1ЃМmЃМ3.
ЁОНтЮіЁП
ЃЈ1ЃЉСюЗжФИВЛЕШгкСуМДПЩЧѓГіБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉАбx=4ДњШыy=![]() +xМДПЩЧѓГіmЕФжЕЃЛ
+xМДПЩЧѓГіmЕФжЕЃЛ
ЃЈ3ЃЉгУЙтЛЌЧњЯпАбИїЕуЫГДЮСЌНгМДПЩЃЛ
ЃЈ4ЃЉИљОнЭМЯёНтД№МДПЩЃЌШчxЃО2ЪБyЫцxЕФдіДѓЖјдіДѓЃЎЃЈД№АИВЛЮЈвЛЃЉЃЛ
ЃЈ5ЃЉИљОнЭМЯёНтД№МДПЩ.
ЃЈ1ЃЉКЏЪ§y=![]() +xЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧxЁй1ЃЎ
+xЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧxЁй1ЃЎ
ЙЪД№АИЮЊxЁй1ЃЎ
ЃЈ2ЃЉx=4ЪБЃЌy=![]() ЃЌ
ЃЌ
Ёрm=![]() ЃЎ
ЃЎ
ЃЈ3ЃЉКЏЪ§ЭМЯѓШчЭМЫљЪОЃК
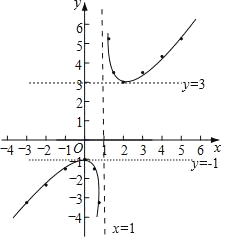
ЃЈ4ЃЉxЃО2ЪБyЫцxЕФдіДѓЖјдіДѓЃЎЃЈД№АИВЛЮЈвЛЃЉ
ЙЪД№АИЮЊЃКxЃО2ЪБyЫцxЕФдіДѓЖјдіДѓЃЎ
ЃЈ5ЃЉЂйИУКЏЪ§ЕФЭМЯѓЙигкЕуЃЈ1ЃЌ1ЃЉГЩжааФЖдГЦЃЛ
ЂкИУКЏЪ§ЕФЭМЯѓгывЛЬѕДЙжБгкxжсЕФжБЯпЮоНЛЕуЃЌдђетЬѕжБЯпЮЊx=1ЃЛ
ЂлжБЯпy=mгыИУКЏЪ§ЕФЭМЯѓЮоНЛЕуЃЌдђmЕФШЁжЕЗЖЮЇЮЊЉ1ЃМmЃМ3ЃЛ
ЙЪД№АИЮЊ1ЃЌ1ЃЌx=1ЃЌЉ1ЃМmЃМ3ЃЛ


 СщаЧМЦЫуаЁДяШЫЯЕСаД№АИ
СщаЧМЦЫуаЁДяШЫЯЕСаД№АИ УЯНЈЦНДэЬтБОЯЕСаД№АИ
УЯНЈЦНДэЬтБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЁЮCDЃЌCEЁЂBEЕФНЛЕуЮЊEЃЌЯжзїШчЯТВйзїЃК
ЕквЛДЮВйзїЃЌЗжБ№зїЁЯABEКЭЁЯDCEЕФЦНЗжЯпЃЌНЛЕуЮЊE1ЃЌ
ЕкЖўДЮВйзїЃЌЗжБ№зїЁЯABE1КЭЁЯDCE1ЕФЦНЗжЯпЃЌНЛЕуЮЊE2ЃЌ
ЕкШ§ДЮВйзїЃЌЗжБ№зїЁЯABE2КЭЁЯDCE2ЕФЦНЗжЯпЃЌНЛЕуЮЊE3ЃЌЁЃЌ
ЕкnДЮВйзїЃЌЗжБ№зїЁЯABEnЉ1КЭЁЯDCEnЉ1ЕФЦНЗжЯпЃЌНЛЕуЮЊEnЃЎ
ШєЁЯEn=1ЖШЃЌФЧЁЯBECЕШгкЁЁ ЁЁЖШ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЕШБп![]() жаЃЌЕуDЁЂEЗжБ№дкБпBCЁЂABЩЯЃЌЧв
жаЃЌЕуDЁЂEЗжБ№дкБпBCЁЂABЩЯЃЌЧв![]() ЃЌADгыCEНЛгкЕуFЃЌдђ
ЃЌADгыCEНЛгкЕуFЃЌдђ![]() ЕФЖШЪ§ЮЊ
ЕФЖШЪ§ЮЊ![]() ЁЁЁЁ
ЁЁЁЁ![]()

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊP(3ЃЌ3)ЃЌЕуBЁЂAЗжБ№дкxжсе§АыжсКЭyжсе§АыжсЩЯЃЌЁЯAPBЃН90ЁуЃЌдђOAЃЋOBЃН________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
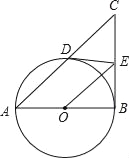
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯABC=90ЁуЃЌвдABЮЊжБОЖЕФЁбOгыACБпНЛгкЕуDЃЌЙ§ЕуDзїЁбOЕФЧаЯпНЛBCгкЕуEЃЌСЌНгOE
(1)жЄУїOEЁЮADЃЛ
(2)ЂйЕБЁЯBAC=ЁЁ ЁЁЁуЪБЃЌЫФБпаЮODEBЪЧе§ЗНаЮЃЎ
ЂкЕБЁЯBAC=ЁЁ ЁЁЁуЪБЃЌAD=3DEЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§бЇПЮЩЯеХРЯЪІНЋПЮБО44вГЕк4ЬтНјааСЫИФБрЃЌЭМаЮВЛБфЃЎЧыФуЭъГЩЯТЮЪЬтЃЎ


ЃЈ1ЃЉШчЭМ1ЃЌЁЯACB=ЁЯADBЃЌBC=BDЃЌЧѓжЄЃКЁїABCЁеЁїABDЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЁЯCAB=ЁЯDABЃЌBC=BDЃЌЧѓжЄЃКЁїABCЁеЁїABDЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCгыЁїDBCжаЃЌЁЯACBЃНЁЯDBCЃН90ЁуЃЌEЪЧBCЕФжаЕуЃЌEFЁЭABЃЌABЃНDEЃЎ
ЃЈ1ЃЉЧѓжЄЃКBCЃНDBЃЛ
ЃЈ2ЃЉШєBDЃН8cmЃЌЧѓACЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧЖЈвхЃКШчЙћвЛИіШ§НЧаЮвЛЬѕБпЩЯЕФИпЕШгкетЬѕБпЃЌФЧУДетИіШ§НЧаЮНазіЁАЕШИпЕзЁБШ§НЧаЮЃЌетЬѕБпНазіетИіШ§НЧаЮЕФЁАЕШЕзЁБЃЎ

ЃЈ1ЃЉИХФюРэНтЃК
ШчЭМ1ЃЌдкЁїABCжаЃЌAC=6ЃЌBC=3ЃЌЁЯACB=30ЁуЃЌЪдХаЖЯЁїABCЪЧЗёЪЧЁБЕШИпЕзЁБШ§НЧаЮЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉЮЪЬтЬНОПЃК
ШчЭМ2ЃЌЁїABCЪЧЁАЕШИпЕзЁБШ§НЧаЮЃЌBCЪЧЁБЕШЕзЁБЃЌзїЁїABCЙигкBCЫљдкжБЯпЕФЖдГЦЭМаЮЕУЕНЁїA'BCЃЌСЌНсAAЁфНЛжБЯпBCгкЕуDЃЎШєЕуBЪЧЁїAAЁфCЕФжиаФЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ3ЃЉгІгУЭиеЙЃК
ШчЭМ3ЃЌвбжЊl1ЁЮl2ЃЌl1гыl2жЎМфЕФОрРыЮЊ2ЃЎЁАЕШИпЕзЁБЁїABCЕФЁАЕШЕзЁБBCдкжБЯпl1ЩЯЃЌЕуAдкжБЯпl2ЩЯЃЌгавЛБпЕФГЄЪЧBCЕФ![]() БЖЃЎНЋЁїABCШЦЕуCАДЫГЪБеыЗНЯђа§зЊ45ЁуЕУЕНЁїA'B'CЃЌAЁфCЫљдкжБЯпНЛl2гкЕуDЃЎЧѓCDЕФжЕЃЎ
БЖЃЎНЋЁїABCШЦЕуCАДЫГЪБеыЗНЯђа§зЊ45ЁуЕУЕНЁїA'B'CЃЌAЁфCЫљдкжБЯпНЛl2гкЕуDЃЎЧѓCDЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШбќЁїABCжаЃЌAB=ACЃЌЁЯACB=72ЁуЃЌ

ЃЈ1ЃЉШєBDЁЭACгкDЃЌЧѓЁЯABDЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєCEЦНЗжЁЯACBЃЌЧѓжЄЃКAE=BCЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com