
【题目】如图,已知![]() 与
与![]() 相交于
相交于![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,且
,且![]() .
.

(1)求证:![]() ;
;
(2)连接![]() ,判断
,判断![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)证明见解析;(2)△NBD是等边三角形,理由见解析.
【解析】
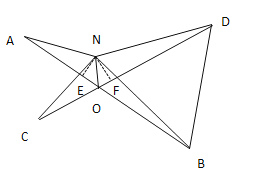
(1)过N作NE⊥AB于E,NF⊥CD于F.根据角平分线上的点到角两边的距离相等,得到NE=NF,根据"HL"证明Rt△AEN≌Rt△CFN,根据全等三角形对应角相等即可得出结论.
(2)设CD、NB相交于点P.证明△ANB≌△CND,根据全等三角形对应角相等、对应边相等得到∠NBA=∠NDC,NB=ND.根据对顶角相等得到∠AOC=60°.在△OPB和△NPD中,利用三角形内角和为180°,可得到∠PND=60°.根据有一个角为60°的等腰三角形是等边三角形即可得出结论.
(1)过N作NE⊥AB于E,NF⊥CD于F.
∵ON平分∠AOD,NE⊥AB,NF⊥CD,
∴NE=NF,∠AEN=∠CFN=90°.
在Rt△AEN和Rt△CFN中,
∵AN=CN,NE=NF,
∴Rt△AEN≌Rt△CFN(HL),
∴∠A=∠C.
(2)△NBD是等边三角形.理由如下:
设CD、NB相交于点P.
在△ANB和△CND中,∵AN=CN,∠A=∠C,AB=CD,
∴△ANB≌△CND(SAS),
∴∠NBA=∠NDC,NB=ND.
∵∠AOC=60°,
∴∠POB=∠AOC=60°.
在△OPB和△NPD中,
∵∠OPB=∠NPD,∠NBA=∠NDC,
∴∠POB=∠PND=60°.
∵NB=ND,∠BND=60°,
∴△NBD是等边三角形.


科目:初中数学 来源: 题型:
【题目】已知一次函数y=x+4的图象与二次函数y=ax(x﹣2)的图象相交于A(﹣1,b)和B,点P是线段AB上的动点(不与A、B重合),过点P作PC⊥x轴,与二次函数y=ax(x﹣2)的图象交于点C.

(1)求a、b的值
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化生活环境,小兰的爸爸要在院墙外的一块空地上修建一个矩形花圃.如图所示,矩形花圃的一边利用长10米的院墙,另外三条边用篱笆围成,篱笆的总长为32米.设AB的长为x米,矩形花圃的面积为y平方米.
(1)用含有x的代数式表示BC的长,BC= ;
(2)求y与x的函数关系式,写出自变量x的取值范围;
(3)当x为何值时,y有最大值?最大值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△![]() C;平移△ABC,若A的对应点
C;平移△ABC,若A的对应点![]() 的坐标为(0,4),画出平移后对应的△
的坐标为(0,4),画出平移后对应的△![]() ;
;
(2)若将△![]() C绕某一点旋转可以得到△
C绕某一点旋转可以得到△![]() ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(3)在![]() 轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过整式乘法的学习,我们进一步了解了利用图形面积来说明法则、公式等的正确性的方法,例如利用图甲可以对平方差公式![]() 给予解释.图乙中的
给予解释.图乙中的![]() 是一个直角三角形,
是一个直角三角形,![]() ,人们很早就发现直角三角形的三边
,人们很早就发现直角三角形的三边![]() 满足
满足![]() 的关系.图丙是2002年国际数学家大会的会徽,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为
的关系.图丙是2002年国际数学家大会的会徽,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为![]() ,较长直角边长为
,较长直角边长为![]() ,求出
,求出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中 ,
中 ,![]() 平分
平分![]() 交
交![]() 于
于![]() ,
,![]() 的两边分别与
的两边分别与![]() ,
, ![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)如图,若![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() .
.
①写出![]() °,
°,![]() 的长是 .
的长是 .
②求四边形![]() 的周长.
的周长.

(2)如图,过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,先补全图乙再证明
,先补全图乙再证明![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市有三个景区是人们节假日游玩的热点景区,某学校对七(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了如下不完全的条形统计图和扇形统计图,请结合图中信息解答下列问题:
(1)九(1)班现有学生__________人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为__________;
(2)请将条形统计图补充完整;
(3)若该校七年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
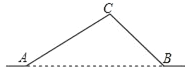
【题目】如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
(参考数据:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com