
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.
(1)如图1,求证:AE=DF;
(2)如图2,若AB=2,过点M作MG⊥EF交线段BC于点G,判断△GEF的形状,并说明理由;
(3)如图3,若AB=![]() ,过点M作MG⊥EF交线段BC的延长线于点G.
,过点M作MG⊥EF交线段BC的延长线于点G.
①直接写出线段AE长度的取值范围;
②判断△GEF的形状,并说明理由.

【答案】(1)见解析;(2)见解析;(3)①![]() <AE≤
<AE≤![]() ;②△GEF是等边三角形,见解析;
;②△GEF是等边三角形,见解析;
【解析】
(1)由条件可以得出AM=DM,∠A=∠ADF=90°,∠AME=∠DMF,可以证明△AEM≌△DFM,就可以得出结论.
(2)过点G作GH⊥AD于H,通过条件可以证明△AEM≌△HMG,得出ME=MG,进而得出∠EGM=45°,再由(1)的结论可以得出∠EGF=90°,从而得出结论.
(3)①当点G、C重合时利用三角形相似就可以求出AE的值,从而求出AE的取值范围.
②过点G作GH⊥AD交AD延长线于点H,证明△AEM∽△HMG,可以得出![]() ,从而求出tan∠MEG=
,从而求出tan∠MEG=![]() ,就可以求出∠MEG=60°,就可以得出结论.
,就可以求出∠MEG=60°,就可以得出结论.
解:(1)如图1,
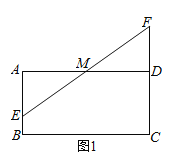
证明:在矩形ABCD中,∠EAM=∠FDM=90°,∠AME=∠FMD.
∵AM=DM,
∴△AEM≌△DFM.
∴AE=DF.
(2)答:△GEF是等腰直角三角形.
证明:过点G作GH⊥AD于H,如图2,

∵∠A=∠B=∠AHG=90°,
∴四边形ABGH是矩形.
∴GH=AB=2.
∵MG⊥EF,
∴∠GME=90°.
∴∠AME+∠GMH=90°.
∵∠AME+∠AEM=90°,
∴∠AEM=∠GMH.
∴△AEM≌△HMG.
∴ME=MG.
∴∠EGM=45°.
由(1)得△AEM≌△DFM,
∴ME=MF.
∵MG⊥EF,
∴GE=GF.
∴∠EGF=2∠EGM=90°.
∴△GEF是等腰直角三角形.
(3)①当C、G重合时,如图3
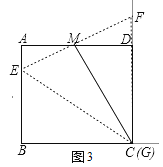 ,
,
∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∴∠AME+∠AEM=90°.
∵MG⊥EF,
∴∠EMG=90°.
∴∠AME+∠DMC=90°,
∴∠AEM=∠DMC,
∴△AEM∽△DMC
∴![]() ,
,
∴![]() ,
,
∴AE=![]()
∴![]() <AE≤
<AE≤![]() .
.
②△GEF是等边三角形.
证明:过点G作GH⊥AD交AD延长线于点H,如图4,
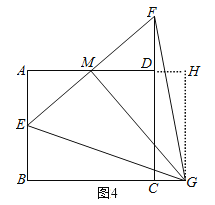
∵∠A=∠B=∠AHG=90°,
∴四边形ABGH是矩形.
∴GH=AB=2![]() .
.
∵MG⊥EF,
∴∠GME=90°.
∴∠AME+∠GMH=90°.
∵∠AME+∠AEM=90°,
∴∠AEM=∠GMH.
又∵∠A=∠GHM=90°,
∴△AEM∽△HMG.
∴![]() .
.
在Rt△GME中,
∴tan∠MEG=![]() =
=![]() .
.
∴∠MEG=60°.
由(1)得△AEM≌△DFM.
∴ME=MF.
∵MG⊥EF,
∴GE=GF.
∴△GEF是等边三角形.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】济宁某校为了解九年级学生艺术测试情况.以九年极(1)班学生的艺术测试成绩为样本,按![]() 、
、![]() 、
、![]() 、
、![]() 四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:

(说明:![]() 级:90分~100分;
级:90分~100分;![]() 级:75分~89分;
级:75分~89分;![]() 级60分~74分;
级60分~74分;![]() 级:60分以下)
级:60分以下)
(1)此次抽样共调查了多少名学生?
(2)请求出样本中![]() 级的学生人数,井补全条形统计图;
级的学生人数,井补全条形统计图;
(3)若该校九年级有1000名学生,请你用此样本估计艺术测试中分数不低于75分的学生人数,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,圆柱体铅笔插入卷笔刀充分卷削,得到底面直径BC为2的圆锥,∠BAC=30°.底面边长为1的正六棱柱铅笔插入卷削,得到如图2所示铅笔和锯齿状木屑(木屑厚度忽略不计),木屑锯齿齿锋点G相邻凹陷最低点为H,则AG=________,GH=________.
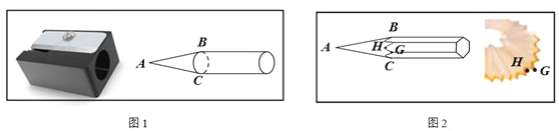
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
| a |
| 12 |
| b |
| 10 |
学生立定跳远测试成绩的频数分布直方图
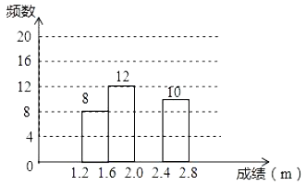
请根据图表中所提供的信息,完成下列问题:
(1)表中![]() ________,
________,![]() ________;
________;
(2)样本成绩的中位数落在________范围内;
(3)请把频数分布直方图补充完整;
(4)该校共有1200名学生,估计该学校学生立定跳远成绩在![]() 范围内的有多少人?
范围内的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
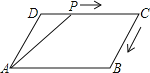
【题目】如图,在平行四边形ABCD中,∠DAB=60°,AB=5,BC=3,点P从点D出发,沿DC,CB向终点B匀速运动.设点P所走过的路程为x,点P所经过的线段与AD,AP所围成的图形的面积为y,y随x的变化而变化.在下列图象中,能正确反映y与x的函数关系的是( )
A.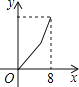 B.
B. C.
C.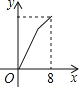 D.
D.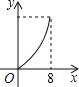
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了防范新冠肺炎疫情,某校在网络平台开展防疫宣传,并出了6道选择题,对甲、乙两个班级学生(各有40名学生)的答题情况进行统计分析,得到统计表如下:
答对的题数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
甲班 | 0 | 2 | 3 | 4 | 17 | 12 | 2 |
乙班 | 0 | 1 | 5 | 3 | 15 | 14 | 2 |
请根据以上信息,解答下列问题:
(1)甲班学生答对的题数的众数为 ;
(2)若答对的题数大于或等于5道的为优秀,则乙班该次考试的优秀率为 ;
(3)从甲、乙两班答题全对的学生中随机抽取2人做学习防疫知识心得交流,通过画树状图或列表法,求抽到的2人来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸条ABCD,AB=5cm,BC=2cm,点M,N分别在边AB,CD上,CN=1cm.现将四边形BCNM沿MN折叠,使点B,C分别落在点B',C'上.当点B'恰好落在边CD上时,线段BM的长为_____cm;在点M从点A运动到点B的过程中,若边MB'与边CD交于点E,则点E相应运动的路径长为_____cm.
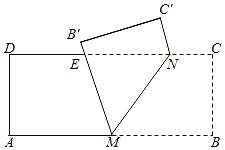
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题情境:如图1,已知等腰直角![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上的一点,且
上的一点,且![]() ,过
,过![]() 作
作![]() 于
于![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() 的长为_______(请直接写出答案)
的长为_______(请直接写出答案)
小明采用如下的做法:
延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,
,
![]() 为
为![]() 中点,
中点,![]() 为
为![]() 的中点,
的中点,
![]() 是
是![]() 的中位线……
的中位线……
请你根据小明的思路完成上面填空;
(2)迁移应用:将图1中的![]() 绕点
绕点![]() 作顺时针旋转,当
作顺时针旋转,当![]() 时,试探究
时,试探究![]() 、
、![]() 、
、![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
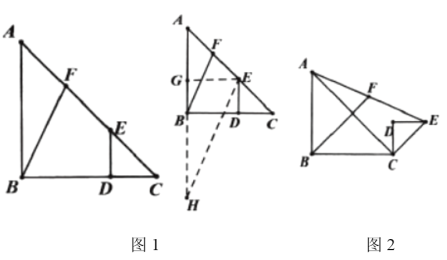
(3)拓展延伸:在旋转的过程中,当![]() 、
、![]() 、
、![]() 三点共线时,直接写出线段
三点共线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com