(1)证明:∵∠A+∠C+∠CDB+∠ABD=360°,∠A=60°,∠CDB=120°,
∴∠C+∠ABD=180°,
∵∠ABD+∠DBF=180°,
∴∠C=∠DBF,
在△DEC和△DFB中,

∴△DEC≌△DFB,
∴DE=DF.
(2)解:CE+BG=EG,
证明:连接DA,
在△ACD和△ABD中
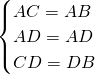
,
∴△ACD≌△ABD,
∴∠CDA=∠BDA=60°,
∵∠EDG=∠EDA+∠ADG=∠ADG+∠GDB=60°,
∴∠CDE=∠ADG,∠EDA=∠GDB,
∵∠BDF=∠CDE,
∴∠GDB+∠BDF=60°,
在△DGF和△DEG中
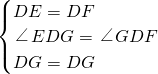
,
∴△DGF≌△DEG,
∴FG=EG,
∵CE=BF,
∴CE+BG=EG.

(3)解:∠EDG=

(180°-α),
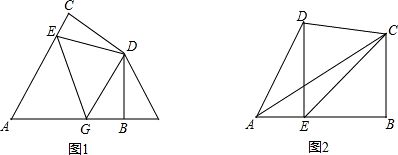
(4)解:过C作CM⊥AD交AD的延长线于M,
在△AMC和△ABC中

,
∴△AMC≌△ABC,
∴AM=AB.CM=BC,
由(1)(2)(3)可知:DM+BE=DE,
∵AE=3,∠AED=90°,∠DAB=60°,
∴AD=6,
由勾股定理得:DE=3

,
∴DM=AB-6=BE+3-6=BE-3,
∴BE-3+BE=3

,
即BE=

(3

+3).
分析:(1)根据已知推出∠C=∠DBF,根据SAS证△DEC≌△DFB即可;
(2)连接AD,根据SSS证△ACD≌△ABD,推出∠CDA=∠BDA=60°,推出∠GDF=60°,得出△DGF≌△DEG,推出FG=EG即可;
(3)根据(1)(2)即可猜出结论;
(4)过C作CM⊥AD交AD的延长线于M,根据全等三角形的性质得出AM=AB,BC=CM,根据结论得出BE+DM=DE,根据勾股定理求出DE,代入即可.
点评:本题综合考查了全等三角形的性质和判定,含30度角的直角三角形性质,勾股定理等知识点的应用,此题是一道综合性比较强的题目,有一定的难度,能根据题意推出规律是解此题的关键.


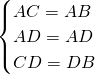 ,
,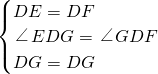 ,
,
 (180°-α),
(180°-α), ,
, ,
, ,
, (3
(3 +3).
+3).
