
分析 设购进价为a元,按原定价销售x件,节日让利销售y件,则淡季销售(1000-x-y)件,根据使全部商品售完后赢利,可得原价销售的价格+节日让利销售的价格+淡季销售的价格≥进价.
解答 解:设购进价为a元,按原定价销售x件,节日让利销售y件,则淡季销售(1000-x-y)件,依题意:
125%ax+125%(1-10%)ay+125%×60%a(1000-x-y)>1000a
即:4x+3y>2000,
∵y≤100,
∴4x>2000-3y≥1700,
又x是整数,∴x≥425.
所以,该超市按日常销售价至少销售425件商品才能不亏损.
故答案为:425.
点评 此题主要考查了一元一次不等式组的应用,充分利用“赢利”这一不等关系,赢利即销售金颇大于成本,题目中并没有包含x、y的等量关系,但利用y≤100和不等式的传递性建立关于x的不等式,从而求出x的取值范围.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:选择题
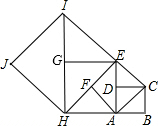 如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第Sn个正方形的面积( )
如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第Sn个正方形的面积( )| A. | 2n | B. | 2n | C. | 2n-1 | D. | 2n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2与-$\frac{1}{2}$ | B. | |-2|与$\frac{1}{2}$ | C. | |-2|与-2 | D. | -|-2|与-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com