
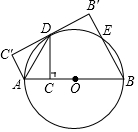
 如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.
如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.分析 (1)连接OD,根据等腰三角形的性质得到∠OAD=∠ADO,根据折叠的性质得到∠C′DA=∠CDA,于是得到结论;
(2)连接AE,BD,由AB是⊙O的直径,得到AE⊥BE,AD⊥BD,推出四边形AEB′C′是矩形,得到AC′=B′E,AE=C′B′,根据折叠的性质得到AC′=AC=3,C′D=CD=$\sqrt{21}$,根据平行线等分线段定理得到AO=BO,得到AE=2$\sqrt{21}$,根据射影定理得到CB=7,由勾股定理即可得到结论.
解答 解:(1)C′D是⊙O的切线,
理由:连接OD,
∵OD=OA,
∴∠OAD=∠ADO,
∵将△ACD沿AD翻折至△AC′D,
∴∠C′DA=∠CDA,
∵CD⊥AB,
∴∠DAC+∠ADC=90°,
∴∠ADO+∠C′DA=90°,
∴OD⊥C′D,
∴C′D是⊙O的切线;
(2)连接AE,BD,
∵AB是⊙O的直径,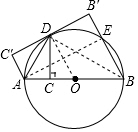
∴AE⊥BE,AD⊥BD,
∵BB′⊥C′D′,
∴∠C′=∠B′=∠AEB′=90°,
∴四边形AEB′C′是矩形,
∴AC′=B′E,AE=C′B′,
∵将△ACD沿AD翻折至△AC′D,
∵AC′=AC=3,C′D=CD=$\sqrt{21}$,
∵AC′⊥C′B′,OD⊥C′B′,
∴AC′∥OD∥BB′,
∵AO=BO,
∴C′B′=2C′D=2$\sqrt{21}$,
∴AE=2$\sqrt{21}$,
∵DC⊥AB,
∴CD2=AC•CB,
∴CB=7,
∴AB=10,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=4.
点评 本题考查了切线的判定,平行线等分线段定理,勾股定理,矩形的判定和性质,射影定理,折叠的性质,正确的作出辅助线是解题的关键.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题
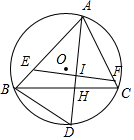 如图,△ABC内接于⊙O,I是△ABC的内心,延长AI交⊙O于D,连接BD,过I作直线EF分别交AB,AC于E,F,且AE=AF.
如图,△ABC内接于⊙O,I是△ABC的内心,延长AI交⊙O于D,连接BD,过I作直线EF分别交AB,AC于E,F,且AE=AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
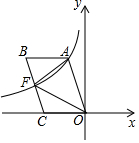 如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例y=$\frac{k}{x}$(k<0)的图象经过点A与BC的中点F,连接AF、OF,若△AOF的面积为9,则k的值为-9.
如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例y=$\frac{k}{x}$(k<0)的图象经过点A与BC的中点F,连接AF、OF,若△AOF的面积为9,则k的值为-9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
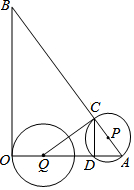 如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动.设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动.设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
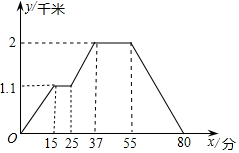 如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为( )
如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为( )| A. | 1.1千米 | B. | 2千米 | C. | 15千米 | D. | 37千米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com