
����Ŀ���ۺ���̽��
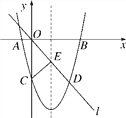
��ͼ����ƽ��ֱ������ϵ�У���֪������y��ax2��bx��8��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��l��������ԭ��O���������ߵ�һ������ΪD���������ߵĶԳ��ύ�ڵ�E������CE����֪��A��D������ֱ�Ϊ(��2��0)��(6����8)��
(1)�������ߵĽ���ʽ�����ֱ������B�͵�E�����ꣻ
(2)��̽�����������Ƿ���ڵ�F��ʹ��FOE�ա�FCE.�����ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1) y��![]() x2��3x��8����2����F������Ϊ(3��
x2��3x��8����2����F������Ϊ(3��![]() ����4)��(3��
����4)��(3��![]() ����4)��
����4)��
�������������������1����A��D������������߿���������ߵĺ�������ʽ���������ߵĶԳ��Կ����B�����꣬��D����������ֱ��OD�Ľ���ʽ��������E�����ꣻ
��2����ϣ�1����֪OE=CE����ȫ�������ε����ʿ�֪OF=CF����֪��F���߶�OC�Ĵ�ֱƽ�����ϣ�������F��������꣬���������߽���ʽ�����F������꣮
���������
��1����������y=ax2+bx-8������A��-2��0����D��6��-8����
��![]()
���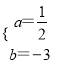
�������ߵĺ�������ʽΪy��![]() x23x8��
x23x8��
��y��![]() x23x8��
x23x8��![]() (x3)2
(x3)2![]() ��
��
�������ߵĶԳ���Ϊֱ��x=3��
����������x�ύ��A��B���㣬��A������Ϊ��-2��0����
���B��������8��0����
��ֱ��L�ĺ�������ʽΪy=kx��
�ߵ�D��6��-8����ֱ��L�ϣ�
��6k=-8�����k=-![]() ��
��
��ֱ��L�ĺ�������ʽΪy=-![]() x��
x��
�ߵ�EΪֱ��L�������߶Գ���Ľ��㣬
���E�ĺ�����Ϊ3��������Ϊ-![]() ��3=-4��
��3=-4��
���E��������3��-4����
��2���������ϴ��ڵ�F��ʹ��FOE�ա�FCE��
��OE=CE=5��
��FO=FC��
���F��OC�Ĵ�ֱƽ�����ϣ���ʱ��F��������Ϊ-4��
��![]() x2-3x-8=-4�����x=3��
x2-3x-8=-4�����x=3��![]() ��
��
���F��������3-![]() ��-4����3+
��-4����3+![]() ��-4����
��-4����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
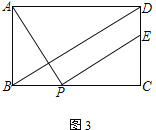
����Ŀ����֪����ABCD����PΪ��BC��һ���㣬����AP�����߶�AP�Ƶ�P˳ʱ����ת90�㣬��Aǡ������ֱ��CD�ϵ�E��
(1) ��ͼ1����E���߶�CD�ϣ���֤��AD��DE��2AB
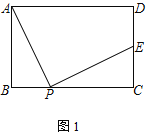
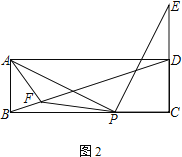
(2) ��ͼ2����E���߶�CD���ӳ����ϣ��ҵ�D Ϊ�߶�CE���е㣬���߶�BD��ȡ��F������AF��PF����AF=AB����֤����APF����ADB
(3) ��ͼ3����E���߶�CD�ϣ�����BD����AB��2��BD��PE����DE��___________ ��ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
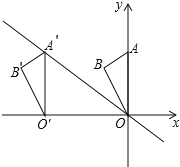
����Ŀ����ͼ����ƽ��ֱ������ϵ�е�A������Ϊ(0��6)����B������Ϊ(��![]() ��5)������AOB��x������ƽ�Ƶõ���A��O��B������A�Ķ�Ӧ��A������ֱ��y����
��5)������AOB��x������ƽ�Ƶõ���A��O��B������A�Ķ�Ӧ��A������ֱ��y����![]() x�ϣ����B�Ķ�Ӧ��B��������Ϊ�� ��
x�ϣ����B�Ķ�Ӧ��B��������Ϊ�� ��
A.(��8��6)B.(��![]() ��5)C.(��
��5)C.(��![]() ��5)D.(��8��5)
��5)D.(��8��5)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�ֶ�������n�ġ�F���㡱������nΪ����ʱ�����Ϊ3n+5������nΪż��ʱ�����Ϊ![]() ������k��ʹ
������k��ʹ![]() Ϊ��������С�������������������ظ����У����磺ȡn��26�������������ͼ��
Ϊ��������С�������������������ظ����У����磺ȡn��26�������������ͼ��
![]()
��ô��n��26ʱ����2016�Ρ�F���㡱�Ľ����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѳ�Ϊ�ҹ���ú�硢ˮ��֮��ĵ������Դ����������Ҫ�����˺�ҶƬ��ɣ���ͼ1����ͼ2�Ǵ�ͼ1������ƽ��ͼ��������վ��A��������˶���C��������55�㣬��HA����ˮƽǰ��43����ɽ��G������ɽ��B����������һҶƬ�������λ�ã���ʱ���ҶƬ�Ķ���D��D��C��H��ͬһֱ���ϣ���������45�㣮��֪ҶƬ�ij���Ϊ35�ף�������ҶƬ���Ӵ��ij��Ⱥ��Բ��ƣ���ɽ��BGΪ10�ף�BG��HG��CH��AH��������CH�ĸߣ����ο����ݣ�tan55���1.4��tan35���0.7��sin55���0.8��sin35���0.6��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ���ͬ�IJ�Ϊ����������ij��������������. �磺2��2��2��(-3)��(-3)��(-3 )��( -3)��. ����������ij˷������ǰ� 2��2��2 ���� 2����������2 ��Ȧ 3 �η���. (-3)��(-3)��(-3 )��( -3)����(-3)����������-3 ��Ȧ 4 �η���.
һ��أ���![]() ��a��0������a��������a ��Ȧc�η���.
��a��0������a��������a ��Ȧc�η���.
(1)ֱ��д����������2��= ��(-3)�� = ��![]() ��= .
��= .
(2)���� 24��23 + (-8)��2��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=��x+2��2+m��ͼ����y�ύ�ڵ�C����B���������ϣ������C���������ߵĶԳ���Գƣ���֪һ�κ���y=kx+b��ͼ���ö��κ���ͼ���ϵĵ�A����1��0������B��
��1������κ�����һ�κ����Ľ���ʽ��
��2������ͼ��д�����㣨x+2��2+m��kx+b��x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC �У���O��AC���ϵ�һ�����㣬����O��ֱ��MN��BC����MN����BCA�Ľ�ƽ�����ڵ�E������BCA�����ƽ�����ڵ�F

��1����֤��EO=FO��
��2������O�˶����δ�ʱ���ı���AECF�Ǿ��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
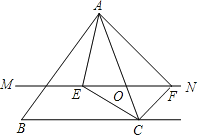
����Ŀ����ͼ���ڡ�ABC�У���O��AC���ϣ��˵���⣩��һ�����㣬����O��ֱ��MN��BC����MN����BCA��ƽ�����ڵ�E������BCA�����ƽ�����ڵ�F������AE��AF����ô����O�˶����δ�ʱ���ı���AECF�Ǿ��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com