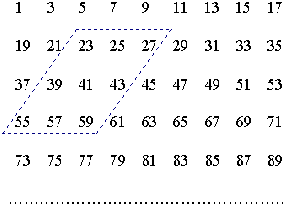
解：（1）每行的第一个数依次为，1，19，37，55，73…
组成了一个首项是1，公差为18的等差数列，
第10项则为：1+（10-1）×18=1+9×18=163，
即第10行第一列的数是163，
所以，第10行第3列的数是163+2+2=167，
故答案为：167．
（2）①、如图，
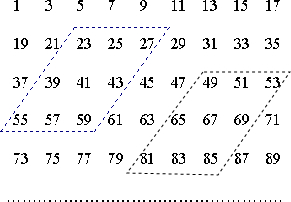
从图中两个平行框可知，
41-23=18，59-41=18，41-27=14，55-41=14，
67-49=18，85-67=18，67-53=14，81-67=14；
…
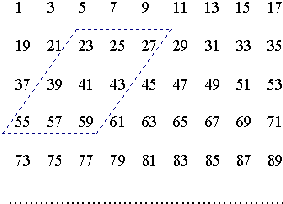
设框中间的数为n，则左上角的数为n-18，左下角的数为n+14，
所以，若这九个数中，中间的数是189，那么左上角的数是189-18=171，
左下角的数是189+14=203；
故答案分别为：171；203．
②根据①的分析和解答，设中间数为n，则这九个数依次是
（n-18），（n-16），（n-14），（n-2），n，（n+2），（n+14），（n+16），（n+18）．
则这9个数之和为9n．
故答案为：九个数之和是中间数的9倍．
③根据②的解答，设中间数为n，可列出方程9n=2007，解得n=223．
因此这9个数分别是，223-18，223-166，223-14，223-2，223，223+2，223+14，223+16，223+18．
故这9个数为：205，207，209，221，223，225，237，239，241．
④设中间数为x，则根据以上得到的规律，可得：9x=2009，则x=223
（不是整数）与假设矛盾．
故：框出的这九个数之和不能等于2009．
分析：（1）根据每行的第一个数依次为，1，19，37，55，73…组成了一个首项是1，公差为18的等差数列，即可求出第10行第一列的数是163，然后即可求出第10行第3列的数．
（2）①、从图中两个平行框可知，有以下规律，设框中间的数为n，则左上角的数为n-18，左下角的数为n+14，然后即可求出答案．
②根据①的分析和解答，设中间数为n，则可得出这九个数排列规律．然后即可知这九个数之和与中间的数的关系．显然，其和为9n．
③根据②的解答，设中间数为n，可列出方程9n=2007，然后解此方程即可．
点评：此题主要考查学生对数字的变化类这一知识点，此题的突破点是；设中间数为n，则这九个数依次是（n-18），（n-16），（n-14），（n-2），n，（n+2），（n+14），（n+16），（n+18）．此题步骤繁琐，难度较大，是一道难题．
