
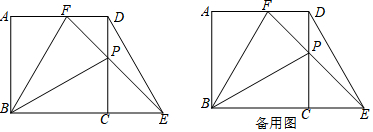
分析 (1)如图1中,延长BP交DE于M.只要证明△BCP≌△DCE,推出∠BCP=∠CDE,由∠CBP+∠CPB=90°,∠CPB=∠DPM,即可推出∠CDE+∠DPM=90°,延长即可解决问题;
(2)根据S1-S2=S△PBE-S△PDE计算即可解决问题;
(3)分两种情形分别求出PC的长,利用(2)中结论计算即可;
解答 解:(1)如图1中,延长BP交DE于M.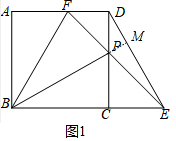
∵四边形ABCD是正方形,
∴CB=CD,∠BCP=∠DCE=90°,
∵CP=CE,
∴△BCP≌△DCE,
∴∠BCP=∠CDE,
∵∠CBP+∠CPB=90°,∠CPB=∠DPM,
∴∠CDE+∠DPM=90°,
∴∠DMP=90°,
∴BP⊥DE.
(2)由题意S1-S2=$\frac{1}{2}$(4+x)•x-$\frac{1}{2}$•(4-x)•x=x2(0<x<4).
(3)①如图2中,当∠PBF=30°时,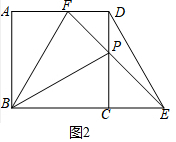
∵∠CPE=∠CEP=∠DPF=45°,∠FDP=90°,
∴∠PFD=∠DPF=45°,
∴DF=DP,∵AD=CD,
∴AF=PC,∵AB=BC,∠A=∠BCP=90°,
∴△BAF≌△BCP,
∴∠ABF=∠CBP=30°,
∴x=PC=BC•tan30°=$\frac{4\sqrt{3}}{3}$,
∴S1-S2=x2=$\frac{16}{3}$.
②如图3中,当∠PBF=45°时,在CB上截取CN=CP,理解PN.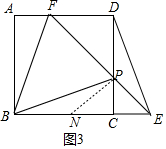
由①可知△ABF≌△BCP,
∴∠ABF=∠CBP,
∵∠PBF=45°,
∴∠CBP=22.5°,
∵∠CNP=∠NBP+∠NPB=45°,
∴∠NBP=∠NPB=22.5°,
∴BN=PN=$\sqrt{2}$x,
∴$\sqrt{2}$x+x=4,
∴x=4$\sqrt{2}$-4,
∴S1-S2=(4$\sqrt{2}$-4)2=48-32$\sqrt{2}$.
点评 本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、勾股定理、三角形的面积、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | a0=0 | B. | a-1=-a | C. | (-a)2=-a2 | D. | a-2=$\frac{1}{{a}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
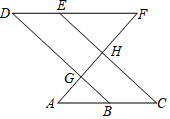 如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.
如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| a | 0.008 | 8 | 8000 | 8000000 |
| $\root{3}{a}$ | 0.2 | 2 | 20 | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
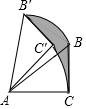 如图,在△ABC中,∠ACB=90°,BC=5,将△ABC绕顶点A按逆时针方向旋转45°至△AB′C′的位置,则线段BC扫过的区域(图中阴影部分)面积为$\frac{25π}{8}$.
如图,在△ABC中,∠ACB=90°,BC=5,将△ABC绕顶点A按逆时针方向旋转45°至△AB′C′的位置,则线段BC扫过的区域(图中阴影部分)面积为$\frac{25π}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com