
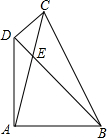
 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=6,则AE=2$\sqrt{6}$.
如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=6,则AE=2$\sqrt{6}$. 分析 根据锐角三角函数和等积法可以求得BD和BD边上的高的长,从而可以求得AE的长.
解答  解:∵∠CDB=90°,∠DCA=30°,
解:∵∠CDB=90°,∠DCA=30°,
∴∠CED=60°,
∴∠AEB=60°,
作AF⊥BD于点F,
∵∠DAB=90°,AB=6,∠ABD=45°,
∴AB=AD=6,
∴BD=6$\sqrt{2}$,
∴AF=$\frac{AB•AD}{BD}=\frac{6×6}{6\sqrt{2}}=3\sqrt{2}$,
∴AE=$\frac{AF}{sin60°}=\frac{3\sqrt{2}}{\frac{\sqrt{3}}{2}}=2\sqrt{6}$,
故答案为:2$\sqrt{6}$.
点评 本题考查锐角三角函数、勾股定理、等积法,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )| A. | 10 | B. | 17 | C. | 20 | D. | 21.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{k=-1}\\{b=1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{k=-1}\\{b=0}\end{array}}\right.$ | C. | $\left\{\begin{array}{l}k=1\\ b=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}k=1\\ b=-4\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )| A. | 前2分钟,乙的平均速度比甲快 | |
| B. | 甲、乙两人8分钟各跑了800米 | |
| C. | 5分钟时两人都跑了500米 | |
| D. | 甲跑完800米的平均速度为100米/分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
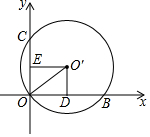 如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴交于点B、C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,OC=6,则⊙O′的半径为( )
如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴交于点B、C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,OC=6,则⊙O′的半径为( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60(x+30)+90x=480 | B. | 60x+90(x+30)=480 | ||
| C. | 60(x+$\frac{30}{60}$)+90x=480 | D. | 60x+90(x+$\frac{30}{60}$)=480 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com