
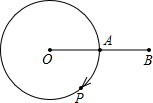
 (2008•南平质检)如图,A是半径为6cm的⊙O上的定点,动点P从A出发,以πcm/s的速度沿圆周按顺时针方向运动,当点P回到A时立即停止运动.设点P运动时间为t(s)
(2008•南平质检)如图,A是半径为6cm的⊙O上的定点,动点P从A出发,以πcm/s的速度沿圆周按顺时针方向运动,当点P回到A时立即停止运动.设点P运动时间为t(s) |
| AP |
| 1 |
| 3 |
| 2 |
| 3 |
 |
| AP |
| nπ×6 |
| 180 |
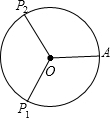 (2)当∠POA=120°时,如图,点P运动的路程为⊙O周长的
(2)当∠POA=120°时,如图,点P运动的路程为⊙O周长的| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
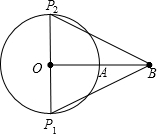 (3)分两种情况:
(3)分两种情况:| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
 ②当∠OPB=90°时,如图,(图中P3处)或(图中P4处),
②当∠OPB=90°时,如图,(图中P3处)或(图中P4处),| 1 |
| 6 |
| 1 |
| 6 |


科目:初中数学 来源:2009年河北省初中毕业生升学文化课模拟考试数学试卷(7)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年浙江省名校中考数学模拟试卷(一)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com