
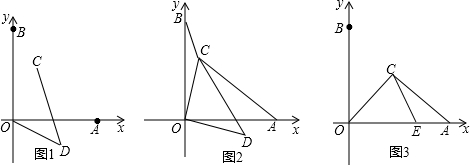
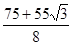 .
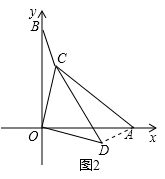
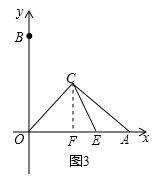
.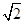 ,根据勾股定理逆定理可证∠ADC=90°,易得∠OCB=∠ODA=135°;
,根据勾股定理逆定理可证∠ADC=90°,易得∠OCB=∠ODA=135°;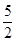 ,再在Rt△CEF中,根据勾股定理求得CF=
,再在Rt△CEF中,根据勾股定理求得CF=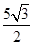 ,然后由三角形的面积公式即可求解.
,然后由三角形的面积公式即可求解.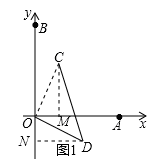
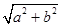 ,
,
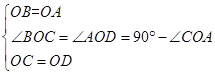 ,
,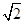 .
.
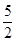 .
.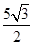 ,
,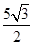 ,
,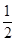 •OA•CF=
•OA•CF=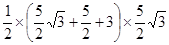 =
=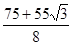 .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源:不详 题型:单选题
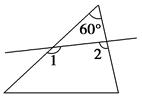
| A.120° | B.180° | C.240° | D.300° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.150° | B.124° |
| C.120° | D.108° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com