��������1���Ƚ�ԭ�㣨0��0�����������ߵĽ���ʽy=��
sin45�㣩x
2-2x+n�У����n��ֵ���������䷽��д�ɶ���ʽ���õ�����B�����꣬Ȼ��������ε����ʣ���֪����AOBC�Ķ���A�붥��B����x��Գƣ��Ӷ������A�����꣬�����������ľ��빫ʽ���ɵõ�����AOBC�ı߳���
��2�����P���˶��ٶ�Ϊÿ��v����λ����t����Q�˶�����BC�ϣ�����ú�vt�Ĵ���ʽ�ֱ��ʾAP��BQ����֤����ARP�ס�BRQ���������������ζ�Ӧ�߳ɱ������vt=
���Ӷ��õ���P�͵�Q�����꣬Ȼ����ݴ���ϵ�����������ֱ��PQ�Ľ���ʽ��
��3���������⣬���������P���Q������ʱ��Ϊ
�룬�ó���ʱ��P���Q��AC���������ٷ���������������ۣ���0��t��
����
��t��2����2��t��
����
��t��
�����ÿһ��������������жϵ�P���Q���ڵ�λ�ã��ٸ��������ʽ���S��t֮��ĺ�����ϵʽ��Ȼ����ݺ��������ʣ�������ֵ��
����⣺��1����������y=��
sin45�㣩x
2-2x+n��ԭ��O��
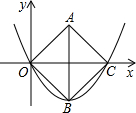
��n=0��
�������ߵĽ���ʽΪy=
x
2-2x��
��y=
x
2-2x=
��x-2
��
2-2
���Ҷ���ΪB��
���B��������2
��-2
����
���ı���AOBC�����Σ�
���A���B����x��Գƣ�
���A��������2
��2
����
������AOBC�ı߳�=
=4��
��2����y=
x
2-2x����y=0����
x
2-2x=0��
���x
1=0��x
2=4
����C��4
��0����
��OC=AB=4
��
������AOBC��������
���AOC=��ABC=45�㣮
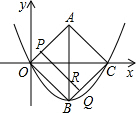
��ͼ�����P���˶��ٶ�Ϊÿ��v����λ����t����Q�˶�����BC�ϣ�
��OP=vt��OB+BQ=3vt��
��AP=4-vt��BQ=3vt-4��
��AR=3
����BR=
��
��AP��BQ�����ARP�ס�BRQ��
��
=
����
=
��
��ã�vt=
��
��OP=
��P��
��
����
BQ=
��Q��
��-
����
��PQ�Ľ���ʽΪy=kx+b�������⣬
�ã�
��
���
��
��PQ�Ľ���ʽΪ��y=-
x+2
��
��3���ߵ�P���˶��ٶ���ÿ��2����λ������Q���˶��ٶ���ÿ��3����λ����
���P���Q������ʱ��Ϊ��
�룬��ʱ��P���Q��AC�ϣ�
�����������
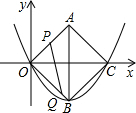
�ٵ�0��t��
ʱ����Q��OB�ϣ���P��OA�ϣ���ͼ��
��OP=2t��OQ=3t����POQ=90�㣬
��S=
OP•OQ=
��2t��3t=3t
2��
��3��0�������߿������ϣ��Գ���Ϊt=0��
���ڶԳ�����Ҳ࣬S��t�����������
�൱t=
ʱ��S�����ֵ����ʱS=3��
=
��
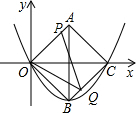
�ڵ�
��t��2ʱ����Q��BC�ϣ���P��OA�ϣ���ͼ��
��OP=2t��
��S=
OP•OB=
��2t��4=4t��
��4��0��
��S��t�����������
�൱t=2ʱ��S�����ֵ����ʱS=4��2=8��
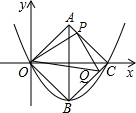
�۵�2��t��
ʱ����Q��BC�ϣ���P��AC�ϣ���ͼ��
��OA+AP=2t��OB+BQ=3t��
��AP=2t-4��BQ=3t-4��
��PC=8-2t��CQ=8-3t��
��S=S
������OACB-S
��OAP-S
��OBQ-S
��PCQ
=16-
��4����2t-4��-
��4����3t-4��-
����8-2t������8-3t��
=-3t
2+10t��
��-3��0�������߿������£��Գ���Ϊt=
=
��
���ڶԳ�����Ҳ࣬S��t���������С��
�൱2��t��
ʱ��S�����ֵ��
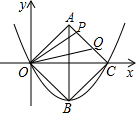
�ܵ�
��t��
ʱ����Q���P����AC�ϣ���ͼ��
��OA+AP=2t��OB+BC+CQ=3t��
��AP=2t-4��CQ=3t-8��
��PQ=AC-AP-CQ=4-��2t-4��-��3t-8��=16-5t��
��S=
PQ•OA=
����16-5t����4=32-10t��
��-10��0��
��S��t�����������
�൱
��t��
ʱ��S�����ֵ��
���Ͽ�֪��S��t֮��ĺ�����ϵʽΪ��S=
| | 3t2(0��t��) | | 4t(��t��2) | | -3t2+10t(2��t��) | | 32-10t(��t��) |
| |
����tΪ2ʱ����OPQ�����������ֵΪ8��

 ��ͼ����֪������y=��
��ͼ����֪������y=�� ��n=0��
��n=0�� ��2����y=
��2����y= ��3���ߵ�P���˶��ٶ���ÿ��2����λ������Q���˶��ٶ���ÿ��3����λ����
��3���ߵ�P���˶��ٶ���ÿ��2����λ������Q���˶��ٶ���ÿ��3����λ���� �ڵ�
�ڵ� �۵�2��t��
�۵�2��t�� �ܵ�
�ܵ�

 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д�
 C��0��3����
C��0��3���� ��C��0��-3�����㣬��x�ύ����һ��B��
��C��0��-3�����㣬��x�ύ����һ��B�� ��2013•��������ͼ����֪�����߾���A��1��0����B��0��3�����㣬�Գ�����x=-1��
��2013•��������ͼ����֪�����߾���A��1��0����B��0��3�����㣬�Գ�����x=-1�� ��ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=1���������߾���A��-1��0����C��0��-3�����㣬��x�ύ����һ��B��
��ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=1���������߾���A��-1��0����C��0��-3�����㣬��x�ύ����һ��B�� ��ͼ����֪������y=ax2+bx+c�Ķ����ǣ�-1��-4��������x�ύ��A��B��1��0�����㣬��y���ڵ�C��
��ͼ����֪������y=ax2+bx+c�Ķ����ǣ�-1��-4��������x�ύ��A��B��1��0�����㣬��y���ڵ�C��