
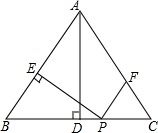
 如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积$\frac{66}{25}$.
如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积$\frac{66}{25}$. 分析 由题意点B′在射线BA上,D′在过D垂直PF的直线上,易知当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的图形是图中平行四边形AD′D″B″.求出D′D″,高DN,即可解决问题.
解答 解:由题意点B′在射线BA上,D′在过D垂直PF的直线上,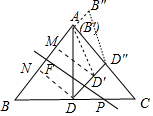
易知当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的图形是图中平行四边形AD′D″B″.
作D′M⊥AB于M,DN⊥AB于N,
在等腰梯形ABDD′中,易知四边形MNDD′是矩形,BN=AM=$\frac{9}{5}$,MN=DD′=5-$\frac{18}{5}$=$\frac{7}{5}$,DN=$\frac{12}{5}$,
∵BD=DC,DD″∥AB,
∴AD″=D″C,
在Rt△ADC中,DD″=$\frac{1}{2}$AC=$\frac{5}{2}$,
∴D′D″=DD″-DD′=$\frac{5}{2}$-$\frac{7}{5}$=$\frac{11}{10}$,
∴当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积=$\frac{11}{10}$×$\frac{12}{5}$=$\frac{66}{25}$,
故答案为$\frac{66}{25}$.
点评 本题考查等腰三角形的性质、轴对称变换、勾股定理、轨迹等知识,解题的关键是学会寻找特殊位置解决问题,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:解答题
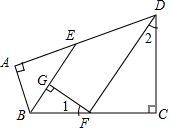 如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?
如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,边长为4的正方形ABCD中,P是BC边上一动点(不含B、C点).将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有①③⑤(写出所有正确结论的序号).
如图,边长为4的正方形ABCD中,P是BC边上一动点(不含B、C点).将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有①③⑤(写出所有正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
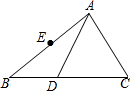 如图,△ABC中,D为BC边上的点,∠CAD=∠CDA,E为AB边的中点.
如图,△ABC中,D为BC边上的点,∠CAD=∠CDA,E为AB边的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com