
 已知如图:Rt△ABC中,∠ACB=90°,AE平分∠BAC,BD平分∠ABC,AE、BD相交于O,OF⊥BD,OH⊥AB.
已知如图:Rt△ABC中,∠ACB=90°,AE平分∠BAC,BD平分∠ABC,AE、BD相交于O,OF⊥BD,OH⊥AB. 分析 (1)由直角三角形的性质和角平分线得出∠OAB+∠OBA=45°,再由三角形的外角性质得出即可得出结果;
(2)延长FO交AB于G,由ASA证明△OBF≌△BOG,得出BF=BG,证出∠2=∠1,由AAS证明△OAG≌△OAD,得出AG=AD,即可得出结论;
(3)作OM⊥BC于M,ON⊥AC于N,则四边形OMCN是矩形,证出∠MOF=∠NOD,由三角形的内心性质得出OM=ON=OH,得出四边形OMCN是正方形,因此CM=CN=OM,由ASA证明△MOF≌△NOD,得出MF=ND,因此CF+CD=CM+CN=2OH,即可得出结果.
解答 (1)证明:∵∠ACB=90°,
∴∠ABC+∠BAC=90°,
∵AE平分∠BAC,BD平分∠ABC,
∴∠OAB=∠OAC=$\frac{1}{2}$∠BAC,∠OBA=∠OBC=$\frac{1}{2}$∠ABC,
∴∠OAB+∠OBA=$\frac{1}{2}$(∠BAC+∠ABC)=45°,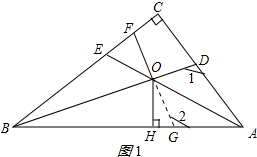
∴∠BOE=∠OAB+∠OBA=45°;
(2)证明:延长FO交AB于G,如图1所示:
∵OF⊥BD,
∴∠BOG=∠BOF=∠FOD=90°,
在△BOF和△BOG中,$\left\{\begin{array}{l}{∠BOF=∠BOG}&{\;}\\{OB=OB}&{\;}\\{∠OBF=∠OBG}&{\;}\end{array}\right.$,
∴△OBF≌△BOG(ASA),
∴BF=BG,
∵OH⊥AB,
∴∠OBA+∠BGO=90°,
∵∠OBC+∠CDB=90°,
∴∠BGO=∠CDB,
∴∠2=∠1,
在△AOG和△AOD中,$\left\{\begin{array}{l}{∠2=∠1}&{\;}\\{∠OAB=∠OAC}&{\;}\\{OA=OA}&{\;}\end{array}\right.$,
∴△OAG≌△OAD(AAS),
∴AG=AD,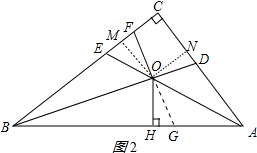
∴BF+AD=BG+AG=AB;
(3)证明:作OM⊥BC于M,ON⊥AC于N,如图2所示:
则四边形OMCN是矩形,
∴∠MON=90°,
∴∠MOF=∠NOD,
∵O是角平分线AE和BD的交点,
∴OM=ON=OH,
∴四边形OMCN是正方形,
∴CM=CN=OM,
在△MOF和△NOD中,$\left\{\begin{array}{l}{∠MOF=∠NOD}&{\;}\\{OM=ON}&{\;}\\{∠OMF=∠OND=90°}&{\;}\end{array}\right.$,
∴△MOF≌△NOD(ASA),
∴MF=ND,
∴CF+CD=CM+CN=2OM=2OH,
∴$\frac{CF+CD}{OH}$=$\frac{2OH}{OH}$=2;
即$\frac{CF+CD}{OH}$为定值.
点评 本题考查了全等三角形的判定与性质、角平分线的性质、矩形的判定与性质、正方形的判定与性质、三角形的内心性质等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
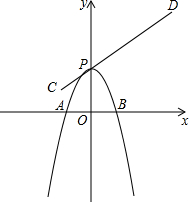 如图,抛物线与x轴相交于A、B两点,在保持抛物线的形状与大小不变的前提下,顶点P在线段CD上移动,点C、D的坐标分别为(-1,1)和(3,4).当顶点P移动到点C时,点B恰好与原点重合.在整个移动过程中,点A移动的距离为( )
如图,抛物线与x轴相交于A、B两点,在保持抛物线的形状与大小不变的前提下,顶点P在线段CD上移动,点C、D的坐标分别为(-1,1)和(3,4).当顶点P移动到点C时,点B恰好与原点重合.在整个移动过程中,点A移动的距离为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |
| B. |
| ||||||||||||||||||||||
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
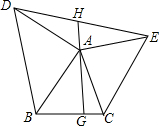 如图,在△ABC中,以A为顶点,以AB、AC为直角三角形的直角边向外侧作等腰直角三角形,连接DE,过A点向BC作垂线AG.反向延长AG交DE于H.
如图,在△ABC中,以A为顶点,以AB、AC为直角三角形的直角边向外侧作等腰直角三角形,连接DE,过A点向BC作垂线AG.反向延长AG交DE于H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com