
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y=��![]() x+4��y�ᡢx��ֱ���
x+4��y�ᡢx��ֱ���
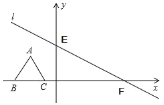
E��F���߳�Ϊ2![]() �ĵȱ���ABC����BC��x���ϣ���������������x���������ƽ�ƣ���ƽ�ƹ����У��õ���A1B1C1������B1��ԭ���غ�ʱ������������⣺
�ĵȱ���ABC����BC��x���ϣ���������������x���������ƽ�ƣ���ƽ�ƹ����У��õ���A1B1C1������B1��ԭ���غ�ʱ������������⣺
��1�������A1�����꣬���жϵ�A1�Ƿ���ֱ��l�ϣ�
��2�������A1C1����ֱ�ߵĽ���ʽ��
��3��������ƽ������һ��P��ʹ����P��A1��C1��FΪ������ı�����ƽ���ı��Σ���ֱ��д��P�����꣮
���𰸡�(1)������;(2) y=��![]() x+6 ;(3) ��P������Ϊ��3
x+6 ;(3) ��P��������3![]() ��3����
��3����![]() ��3����5
��3����5![]() ����3����
����3����
��������
��1������A1��A1D��x���ڵ�D�����ݵȱ������ε����ʿɵó�B1D��A1D�ij��ȣ������ɵó���A1�����꣬������һ�κ���ͼ���ϵ�������������ҳ���A1��ֱ��l�ϣ�
��2���ɵȱ������εı߳����ҳ���C1�����꣬�ɵ�A1��C1�����꣬���ô���ϵ�������������A1C1����ֱ�ߵĽ���ʽ��
��3���ֱ�����A1C1F��������Ϊ�Խ����ҳ�ƽ���ı��Σ�����ƽ���ı��ε����ʼ����ҳ���P�����꣮
��1������A1��A1D��x���ڵ�D����ͼ1��ʾ��
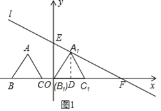
�ߡ�A1B1C1�DZ߳�Ϊ2![]() �ĵȱ������Σ�
�ĵȱ������Σ�
��B1D=![]() ��2
��2![]() =
=![]() ��A1D=
��A1D=![]() ��2
��2![]() =3��
=3��
���A1��������![]() ��3����
��3����
�ߵ�x=![]() ʱ��y=��
ʱ��y=��![]() ��
��![]() +4=3��
+4=3��
���A1��ֱ��l�ϣ�
��2���ߡ�A1B1C1�DZ߳�Ϊ2![]() �ĵȱ������Σ�
�ĵȱ������Σ�
��B1C1=2![]() ��
��
���C1��������2![]() ��0����
��0����
���A1C1����ֱ�ߵĽ���ʽΪy=kx+b��k��0����
��A1��![]() ��3����C1��2
��3����C1��2![]() ��0������y=kx+b���ã�
��0������y=kx+b���ã�
![]() ����ã�
����ã�![]()
���A1C1����ֱ�ߵĽ���ʽΪy=��![]() x+6��
x+6��
��3����y=0ʱ���Щ�![]() x+4=0��
x+4=0��
��ã�x=4![]() ��
��
���F��������4![]() ��0����
��0����
������������ǣ���ͼ2����
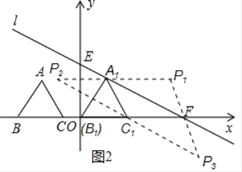
�ٵ�A1FΪ�Խ���ʱ���ı���A1C1FP1Ϊƽ���ı��Σ�
��A1��![]() ��3����C1��2
��3����C1��2![]() ��0����F��4
��0����F��4![]() ��0����
��0����
���P1��������![]() +4
+4![]() ��2
��2![]() ��3+0��0��������3
��3+0��0��������3![]() ��3����
��3����
�ڵ�A1C1Ϊ�Խ���ʱ���ı���A1P2C1FΪƽ���ı��Σ�
��A1��![]() ��3����C1��2
��3����C1��2![]() ��0����F��4
��0����F��4![]() ��0����
��0����
���P2��������![]() +2
+2![]() ��4
��4![]() ��3+0��0����������
��3+0��0����������![]() ��3����
��3����
�۵�C1FΪ�Խ���ʱ���ı���A1C1P3FΪƽ���ı��Σ�
��A1��![]() ��3����C1��2
��3����C1��2![]() ��0����F��4
��0����F��4![]() ��0����
��0����
���P3��������2![]() +4
+4![]() ��
��![]() ��0+0��3��������5
��0+0��3��������5![]() ����3����
����3����
������������P��������3![]() ��3����
��3����![]() ��3����5
��3����5![]() ����3����
����3����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽��
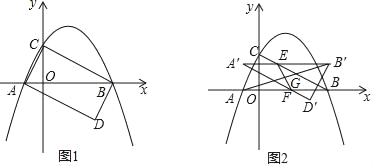
��ͼ1��������y=ax2+bx+2��x�ύ��A����1��0����B��4��0�����㣬��y�ύ�ڵ�C������AC��BC��DΪ����ƽ�����������һ�㣬��ʹ����ABD����ABCȫ�ȣ�
��1���������ߵı���ʽ��
��2����ֱ��д����D�����꣬���ж��ı���ACBD����״��
��3����ͼ2������ABD��y�����������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ��õ���A��B��D�䣬A��B����BC���ڵ�E��A��D����AB���ڵ�F������EF��AB�䣬EF��AB�����ڵ�G�����˶���ʱ��Ϊt��0��t��2���룮
����ֱ��EF���������ߵĶ���Tʱ���������ʱt��ֵ��
����ֱ��д����G������·���ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������OΪԭ���ֱ������ϵ�У������ߵĶ���ΪA��1��4�����Ҿ�����B��2��3������x�ύ��C��D���㣮
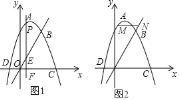
��1����ֱ��OB�ĺ�������ʽ�������ߵĺ�������ʽ��
��2����ͼ1����P��x���Ϸ�����������һ���㣬����P��ֱ��PF��x���ڵ�F����ֱ��OB�ڵ�E����PE=3EF�����P��ĺ����ꣻ
��3����ͼ2����M�������ϵ�һ�����㣬����ֱ��OB���Ϸ�������M��x���ƽ������ֱ��OB���ڵ�N��T�������߶Գ�����һ�㣬��MN�������MDT�ܳ���Сʱ��ֱ��д��T�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ABC�ǵ��������Σ�AB=AC����D��E��F�ֱ���AB��BC��AC���ϣ���BD=CE��BE=CF��
��1����֤����DEF�ǵ��������Σ�
��2�����룺����A����ʲô����ʱ����DEF�ǵȱ������Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AE��BF��ACƽ����BAE���ҽ�BF�ڵ�C��BDƽ����ABF���ҽ�AE�ڵ�D��AC��BD�ཻ�ڵ�O������CD
��1������AOD�Ķ�����
��2����֤���ı���ABCD�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�E��FΪBC�����㣬��BE=CF��AF=DE��
��֤����1����ABF�ա�DCE��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D��AB�ϣ���E��AC�ϣ��ҡ�AEB����ADC����ô��������һ�������������ж���ABE�ա�ACD���ǣ� ��

A.AD��AEB.��B����CC.BE��CDD.AB��AC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1��ֱ��![]() ���ڵ�
���ڵ�![]() ��ֱ��l1�ֱ�x�ᡢy���ڵ�A,B��OB=2��ֱ��l2��x���ڵ�C.
��ֱ��l1�ֱ�x�ᡢy���ڵ�A,B��OB=2��ֱ��l2��x���ڵ�C.

��1����m��ֵ���ı���OBPC�����;
��2����ֱ��l1�Ľ���ʽ;
��3�����Q��ֱ��l2�ϵ�һ���㣬����A��C��QΪ����������ε���������ı���OBPC�����ʱ�����Q������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com