
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=2cm.
![]()
(1)求AC的长
(2)若点E在直线AD上,且EA=3cm,求BE的长
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,观察函数y=|x|的图象,写出它的两条的性质;
(2)在图1中,画出函数y=|x-3|的图象;
根据图象判断:函数y=|x-3|的图象可以由y=|x|的图象向 平移 个单位得到;
(3)①函数y=|2x+3|的图象可以由y=|2x|的图象向 平移 单位得到;
②根据从特殊到一般的研究方法,函数y=|kx+3|(k为常数,k≠0)的图象可以由函数y=|kx|(k为常数,k≠0)的图象经过怎样的平移得到.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
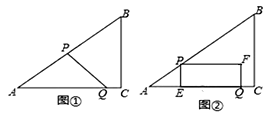
【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒![]() 个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长;(用含t的代数式表示)
(2)连结PQ,当PQ与△ABC的一边平行时,求t的值;
(3)如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF.设矩形PEQF与△ABC重叠部分图形的面积为S.直接写出点P在运动过程中S与t之间的函数关系式和自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
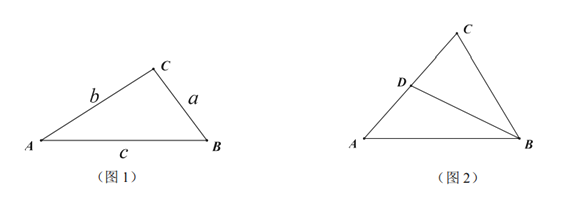
【题目】如图1,![]() 的
的![]() 所对边分别是
所对边分别是![]() ,且
,且![]() ,若满足
,若满足![]() ,则称
,则称![]() 为奇异三角形,例如等边三角形就是奇异三角形.
为奇异三角形,例如等边三角形就是奇异三角形.
(1)若![]() ,判断
,判断![]() 是否为奇异三角形,并说明理由;
是否为奇异三角形,并说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图2,在奇异三角形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,连结
边上的中点,连结![]() ,
,![]() 将
将![]() 分割成2个三角形,其中
分割成2个三角形,其中![]() 是奇异三角形,
是奇异三角形,![]() 是以
是以![]() 为底的等腰三角形,求
为底的等腰三角形,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的边
的边![]() 上有一动点
上有一动点![]() ,从距离
,从距离![]() 点
点![]() 的点
的点![]() 处出发,沿线段
处出发,沿线段![]() ,射线
,射线![]() 运动,速度为
运动,速度为![]() ;动点
;动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 运动,速度为
运动,速度为![]() .
.![]() ,
,![]() 同时出发,设运动时间是
同时出发,设运动时间是![]() .
.

(1)当点![]() 在
在![]() 上运动时,
上运动时,![]()
![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 在
在![]() 上运动时,
上运动时,![]() 为何值,能使
为何值,能使![]() ?
?
(3)若点![]() 运动到距离
运动到距离![]() 点
点![]() 的点
的点![]() 处停止,在点
处停止,在点![]() 停止运动前,点
停止运动前,点![]() 能否追上点
能否追上点![]() ?如果能,求出
?如果能,求出![]() 的值;如果不能,请说出理由.
的值;如果不能,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a﹣30|+(b+6)2=0.点O是数轴原点.
![]()
(1)点A表示的数为 ,点B表示的数为 ,线段AB的长为 .
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为 .
(3)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
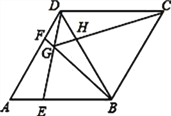
【题目】如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:①△AED≌△DFB; ②S四边形BCDG=![]() CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.
CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com