
����Ŀ����ƽ��ֱ������ϵ�У�����������P��x1��y1����Q��x2��y2��Ϊ�˵���߶ε��е�����Ϊ![]() ��
��
��1����ͼ��1����CΪ�߶�AB�е㣬A������Ϊ��0��4����B������Ϊ��5��4�������C������Ϊ�� ��
��2����ͼ��2����FΪ�߶�DE�е㣬D������Ϊ����4����3����E������Ϊ��1����3�������F������Ϊ________
Ӧ�ã�
��1����ͼ��3����������ONDF�ĶԽ����ཻ�ڵ�M��ON��OF�ֱ���x���y���ϣ�OΪ����ԭ�㣬��D������Ϊ��4��3�������M������Ϊ�� ����
��2����ֱ������ϵ������A����1��2����B��3��1����C��1��4�����㣬����һ��D��A��B��C����ƽ���ı��εĶ��㣬ֱ��д��D�����꣮

���𰸡���1�� (2.5,4)����2��(-1.5,-3)����3��(2,1.5)����4�� (-3,5) ��(1,-1)��(5,3)
��������������(1)�����������и������е�ļ��㷨����м��㼴�ɵó��𰸣�(2)������ƽ���ı��ε����ʷ���ABΪ�Խ�������BCΪ�Խ��ߺ���ACΪ�Խ�����������ֱ�����𰸣�
��⣺(1)��(0+5)��2=2.5��(4+4)��2=4�����C������Ϊ(2.5��4)��
(2)��(��4+1)��2=��1.5�� (��3��3)��2=��3�����F������Ϊ(��1.5����3)��
Ӧ��(1)���߾��εĶԽ�����ƽ�֣� ��(0+4)��2=2�� (0+3)��2=1.5��
���M������Ϊ(2��1.5)��
(2)�����D��������x��y����
����ABΪ�Խ��ߣ�AC��BCΪ�ڱ߹���ƽ���ı��Σ���AB��CD���е��غϣ�
��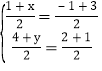 ����ã�
����ã�![]() ��
��
����BCΪ�Խ��ߣ�AB��ACΪ�ڱ߹���ƽ���ı��Σ���AD��BC���е��غ�
��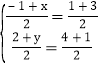 ����ã�
����ã�![]() ��
��
����ACΪ�Խ��ߣ�AB��BCΪ�ڱ߹���ƽ���ı��Σ���BD��AC���е��غ�
��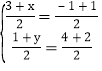 ����ã�
����ã�![]() ��
��
���Ͽ�֪����D������Ϊ��1��-1����5��3����-3��5����


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѽ���ͼ��ƴ��һ���µ�ͼ�Σ���ͨ��ͼ������ļ��㣬�������Եõ�һЩ���õ���Ϣ����������һЩ������ͼ�ε����.
(1)��ͼ1��ʾ����һ�ų�����ֽ�尴ͼ�����߲ü��ɾſ飬�����������DZ߳���Ϊm�Ĵ������Σ������DZ߳���Ϊn��С�����Σ�����dz�Ϊm����Ϊn��ȫ��С�����Σ���m>n.�۲�ͼ�Σ����Է��ִ���ʽ2m2��5mn��2n2������ʽ�ֽ�Ϊ .
(2)��ͼ1��ÿ��С�����ε����Ϊ12cm2���ĸ������ε������Ϊ50 cm2������ͼ�����вü���(���߲���)��֮��.
(3)��ͼ2�б߳�Ϊa��b��������ƴ��һ��B,C,G������ͬһ��ֱ���ϣ�����BD��BF���������������εı߳�����a+b=10��ab=16���������Ӱ���ֵ����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A�������ǣ�4��3������ԲD����A��O���ֱ�����������������ύ�ڵ�E��F����EF��OAʱ����ʱEF= �� 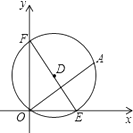
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ֵ��ӻ�ԭ��ÿ̨2600Ԫ�������ڼ��Ծ����۳��ۣ������̼ҹ涨��2000Ԫ��200Ԫ�����������ֵ��ӻ�ʵ����Ҫ����Ǯ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MON=60�㣬���߳�Ϊ1����������A1B1C1D1E1F1 �� ��A1B1��F1E1�ֱ�������OM��ON�ϣ���C1D1���ڵ�ֱ�߷ֱ�OM��ON�ڵ�A2��F2 �� ��A2F2Ϊ������������A2B2C2D2E2F2 �� ��C2D2���ڵ�ֱ�߷ֱ�OM��ON�ڵ�A3��F3 �� ����A3F3Ϊ������������A3B3C3D3E3F3 �� �������˹��ɣ�����n����ͼ��Bn��ON�ľ����� �� 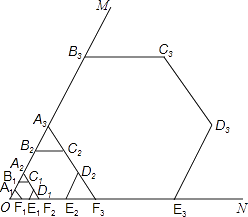
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��![]() ��
��![]() ����֤��
����֤��![]() .
.

֤������![]() ��
��
��________________��ͬ���ڽǻ�������ֱ��ƽ�У���
��![]() =________����ֱ��ƽ�У��ڴ�����ȣ���
=________����ֱ��ƽ�У��ڴ�����ȣ���
�֡�![]() ����֪����
����֪����
��________________���ڴ�����ȣ���ֱ��ƽ�У���
��![]() =________����ֱ��ƽ�У��ڴ�����ȣ���
=________����ֱ��ƽ�У��ڴ�����ȣ���
��![]() -
-![]() =________________��
=________________��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C���߶�AB���е㣬CDƽ����ACE��CEƽ����BCD��CD=CE;

(1)��֤����ACD�ա�BCE;
(2)����D=50��������B�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪l1��l2��MN�ֱ��ֱ��l1��l2���ڵ�A��B��ME�ֱ��ֱ��l1��l2���ڵ�C��D����P��MN�ϣ�P����A��B��M���㲻�غϣ���
��1�������P��A��B����֮���˶�ʱ�����������¡�����֮���к�������ϵ��˵�����ɣ�
��2�������P��A��B��������˶�ʱ�����������¡������к�������ϵ��ֻ��д�����ۣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��AD�ǽ�ƽ���ߣ�BEƽ�֡�ABC��AD�ڵ�E����O��AB�ϣ���OBΪ�뾶�ġ�O������E����AB�ڵ�F 
��1����֤��AD�ǡ�O�����ߣ�
��2����AC=4����C=30�㣬�� ![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com