
【题目】如图,二次函数![]() 为常数,
为常数,![]() ),当
),当![]() 时,
时,![]() .
.
![]() 求
求![]() ;
;
![]() 求此抛物线与
求此抛物线与![]() 轴、
轴、![]() 轴交点;
轴交点;
![]() 画出函数的图象.
画出函数的图象.
【答案】解:![]() ;
; ![]() 与
与![]() 轴交点
轴交点![]() ;与
;与![]() 轴交点:
轴交点:![]() ;
; ![]() 详见解析
详见解析
【解析】
(1)把![]() ,
,![]() 代入即可求出a的值;
代入即可求出a的值;
(2)确定抛物线的关系式后,分别令x=0,求出图像与y轴的交点坐标,令y=0,求出与x轴的交点坐标;
(3)由题意和抛物线的性质可得,抛物线顶点,对称轴,与x轴和y轴的交点,过(1,-5),得出还过(-5,-5)点,根据这些特殊点即可画出其图像.
解:(1)∵当![]() 时,
时,![]()
∴代入![]() 得
得
![]()
解得 a=-1.
(2)∵a=-1
∴该二次函数的解析式为![]()
令y=0,得![]()
解得 ![]()
∴与x轴的交点坐标为(-4,0),(0,0).
令x=0,得![]()
解得 y=0.
∴与y轴的交点坐标为(0,0).
(3)由(2)知:抛物线的对称轴为直线x=-2,与x轴的交点坐标为(-4,0),(0,0),顶点坐标为(-2,4),图像过(1,-5),由对称性可知还过(-5,-5)点,根据这些特殊点可以画出图像,如图所示:
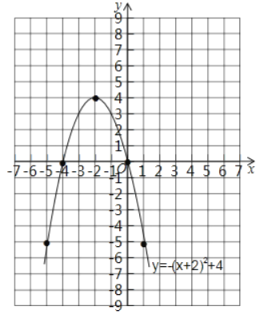
故答案为![]() ;
; ![]() 与
与![]() 轴交点
轴交点![]() ;与
;与![]() 轴交点:
轴交点:![]() ;
; ![]() 详见解析
详见解析


科目:初中数学 来源: 题型:
【题目】某超市欲购进一种今年新上市的产品,购进价为20元![]() 件,为了调查这种新产品的销路,该超市进行了试销售,得知该产品每天的销售量
件,为了调查这种新产品的销路,该超市进行了试销售,得知该产品每天的销售量![]() 件
件![]() 与每件的销售价
与每件的销售价![]() 元
元![]() 件
件![]() 之间有如下关系:
之间有如下关系:![]()
![]() 请写出该超市销售这种产品每天的销售利润
请写出该超市销售这种产品每天的销售利润![]() 元
元![]() 与x之间的函数关系式,并求出超市能获取的最大利润是多少元.
与x之间的函数关系式,并求出超市能获取的最大利润是多少元.
![]() 若超市想获取1500元的利润
若超市想获取1500元的利润![]() 求每件的销售价.
求每件的销售价.
![]() 若超市想获取的利润不低于1500元,请求出每件的销售价X的范围?
若超市想获取的利润不低于1500元,请求出每件的销售价X的范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=2,BC=3.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于![]() PQ的长为半径画弧,两弧相交于点N,射线CN交AD与点F,交BA的延长线于点E,则三角形CDF与四边形AFCB的面积比是( )
PQ的长为半径画弧,两弧相交于点N,射线CN交AD与点F,交BA的延长线于点E,则三角形CDF与四边形AFCB的面积比是( )
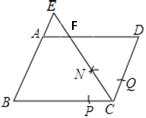
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是长方体模型,棱长如图所示,图2是它的一种表面展开图.
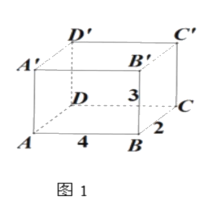
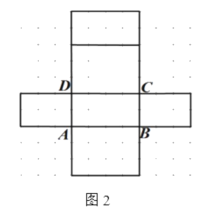

(1)①在图2中,表示出C可能的位置;
②在图3中画出长方体的一种展开图(不同于图2);
(2)图1中,一只在顶点A的蚂蚁,要吃到C处的甜食,求它沿长方体表面爬行的最短距离;
(3) 在满足AB+BC+BB=9的条件下,当AB为何值时,蚂蚁从A沿长方体表面爬行到C距离最短,并写出其中的一种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
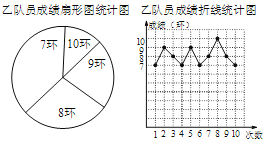
【题目】某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛,特为甲、乙两名队员举行了一次选拔赛,要求这两名队员各射击10次.比赛结束后,根据比赛成绩情况,将甲、乙两名队员的比赛成绩制成了如下的统计图(表):
甲队员的成绩统计表
成绩(单位:环) | 7 | 8 | 9 | 10 |
次数(单位:次) | 5 | 1 | 2 | 2 |
(1)在图1中,求“8环”所在扇形的圆心角的度数;
(2)经过整理,得到的分析数据如表,求表中的a、b、c的值.
队员 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 8 | 7.5 | 7 | c |
乙 | a | b | 7 | 1 |
(3)根据甲、乙两名队员的成绩情况,该射击队准备选派乙参加比赛,请你写出一条射击队选派乙的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
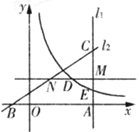
【题目】如图,直线 ![]() 经过点
经过点![]() ,且垂直于
,且垂直于![]() 轴,直线
轴,直线![]() 经过点
经过点![]() ,与
,与![]() 交于点
交于点![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上一点,直线
上一点,直线![]() 轴,交
轴,交![]() 于点
于点![]() 是
是![]() 的中点,双曲线
的中点,双曲线![]() 经过点
经过点![]() ,与
,与![]() 交于点
交于点![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)当点![]() 是
是![]() 的中点时,求点
的中点时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校为创建书香校园,4月份购进一批图书,经了解,科普书的单价比文学书的单价多4元,用1500元购进的科普书与1000元购进的文学书本数相等.
(1)求4月份购进的科普书和文学书的单价各是多少元?
(2)若5月份科普书和文学书的单价与4月份相比保持不变,我校现打算用1250元再购进一批科普书和文学书,问购进科普书65本后至多还能购进多少本文学书?
查看答案和解析>>
科目:初中数学 来源: 题型:
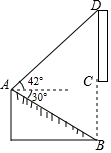
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com