
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时点Q从点B出发沿BC边向点C以每秒2cm的速度移动P、Q两点在分别到达B、C两点后就停止移动,设两点移动的时间为t秒,回答下列问题:
(1)如图1,当t为几秒时,△PBQ的面积等于5cm2?
(2)如图2,当t=![]() 秒时,试判断△DPQ的形状,并说明理由;
秒时,试判断△DPQ的形状,并说明理由;
(3)如图3,以Q为圆心,PQ为半径作⊙Q.
①在运动过程中,是否存在这样的t值,使⊙Q正好与四边形DPQC的一边(或边所在的直线)相切?若存在,求出t值;若不存在,请说明理由;
②若⊙Q与四边形DPQC有三个公共点,请直接写出t的取值范围。

【答案】(1)1秒或5秒(2)直角三角形(3)①t=0或t=﹣18+12![]() ②0<t<6
②0<t<6![]() ﹣18
﹣18
【解析】试题分析:(1)由题意可知PA=t,BQ=2t,从而得到PB=6﹣t,BQ=2t,然后根据△PQB的面积=5cm2列方程求解即可;
(2)由t=![]() ,可求得AP=
,可求得AP=![]() ,QB=3,PB=
,QB=3,PB=![]() ,CQ=9,由勾股定理可证明DQ2+PQ2=PD2,由勾股定理的逆定理可知△DPQ为直角三角形;
,CQ=9,由勾股定理可证明DQ2+PQ2=PD2,由勾股定理的逆定理可知△DPQ为直角三角形;
(3)①当t=0时,点P与点A重合时,点B与点Q重合,此时圆Q与PD相切;当⊙Q正好与四边形DPQC的DC边相切时,由圆的性质可知QC=QP,然后依据勾股定理列方程求解即可;
②先求得⊙Q与四边形DPQC有两个公共点时t的值,然后可确定出t的取值范围.
试题解析:(1)∵当运动时间为t秒时,PA=t,BQ=2t,
∴PB=6﹣t,BQ=2t.
∵△PBQ的面积等于5cm2,
∴![]() PBBQ=
PBBQ=![]() (6﹣t)2t.
(6﹣t)2t.
∴![]() .
.
解得:t1=1,t2=5.
答:当t为1秒或5秒时,△PBQ的面积等于5cm2.
(2)△DPQ的形状是直角三角形.
理由:∵当t=![]() 秒时,AP=
秒时,AP=![]() ,QB=3,
,QB=3,
∴PB=6﹣![]() =
=![]() ,CQ=12﹣3=9.
,CQ=12﹣3=9.
在Rt△PDA中,由勾股定理可知:PD2=DA2+PA2=122+(![]() )2=
)2=![]() .
.
同理:在Rt△PBQ和Rt△DCQ中由勾股定理可得:DQ2=117,PQ2=![]() .
.
∵117+![]() =
=![]() ,
,
∴DQ2+PQ2=PD2.
所以△DPQ的形状是直角三角形.
(3span>)①(Ⅰ)由题意可知圆Q与AB、BC不相切.
(Ⅱ)如图1所示:当t=0时,点P与点A重合时,点B与点Q重合.

∵∠DAB=90°,
∴∠DPQ=90°.
∴DP⊥PQ.
∴DP为圆Q的切线.
(Ⅲ)当⊙Q正好与四边形DPQC的DC边相切时,如图2所示.

由题意可知:PB=6﹣t,BQ=2t,PQ=CQ=12﹣2t.
在Rt△PQB中,由勾股定理可知:PQ2=PB2+QB2,即(6﹣t)2+(2t)2=(12﹣2t)2.
解得:t1=﹣18+12![]() ,t2=﹣18﹣12
,t2=﹣18﹣12![]() (舍去).
(舍去).
综上所述可知当t=0或t=﹣18+12![]() 时,⊙Q与四边形DPQC的一边相切.
时,⊙Q与四边形DPQC的一边相切.
②(Ⅰ)当t=0时,如图1所示:⊙Q与四边形DPQC有两个公共点;
(Ⅱ)如图3所示:当圆Q经过点D时,⊙Q与四边形DPQC有两个公共点.
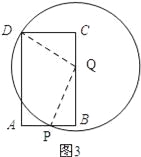
由题意可知:PB=6﹣t,BQ=2t,CQ=12﹣2t,DC=6.
由勾股定理可知:DQ2=DC2+CQ2=62+(12﹣2t)2,PQ2=PB2+QB2=(6﹣t)2+(2t)2.
∵DQ=PQ,
∴DQ2=PQ2,即62+(12﹣2t)2=(6﹣t)2+(2t)2.
整理得:t2+36t﹣144=0.
解得:t1=6![]() ﹣18,t2=﹣6
﹣18,t2=﹣6![]() ﹣18(舍去).
﹣18(舍去).
∴当0<t<6![]() ﹣18时,⊙Q与四边形DPQC有三个公共点.
﹣18时,⊙Q与四边形DPQC有三个公共点.


科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 80° B. 90° C. 100° D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC中,点D、E、F分别为AB、BC、CA上的点,且AD=BE=CF.
(1)△DEF是__________三角形;
(2)如图2,M为线段BC上一点,连接FM,
在FM的右侧作等边△FMN,连接DM、EN.求证:DM=EN;
(3)如图3,将上题中“M为线段BC上一点”改为“点M为CB延长线上一点”,其余条件不变,求证:DM=EN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2
(1)求实数k的取值范围。
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师做了个长方形教具,其中一边长为2a+b,另一边长为a﹣b,则该长方形的面积为( )
A.6a+b
B.2a2﹣ab﹣b2
C.3a
D.10a﹣b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的大小;
(2)若CD=3,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com