
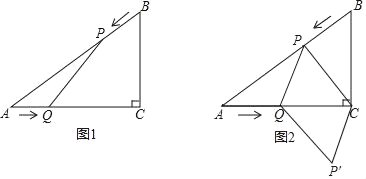
【题目】已知:如图1在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点P由点B出发沿BA方向向点A匀速运动,速度为2cm/s;同时点Q由点A出发沿AC方向点C匀速运动,速度为lcm/s;连接PQ,设运动的时间为t秒(0<t<5),解答下列问题:
(1)当为t何值时,PQ∥BC;
(2)设△AQP的面积为y(cm2),求y关于t的函数关系式,并求出y的最大值;
(3)如图2,连接PC,并把△PQC沿QC翻折,得到四边形PQPC,是否存在某时刻t,使四边形PQP'C为菱形?若存在,求出此时t的值;若不存在,请说明理由.
【答案】(1)当t=![]() 时,PQ∥BC;(2)﹣
时,PQ∥BC;(2)﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,当t=
,当t=![]() 时,y有最大值为
时,y有最大值为![]() ;(3)存在,当t=
;(3)存在,当t=![]() 时,四边形PQP′C为菱形
时,四边形PQP′C为菱形
【解析】
(1)只要证明△APQ∽△ABC,可得![]() =
=![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
(2)过点P作PD⊥AC于D,则有△APD∽△ABC,理由相似三角形的性质构建二次函数即可解决问题;
(3)存在.由△APO∽△ABC,可得![]() =
=![]() ,即
,即![]() =
=![]() ,推出OA=
,推出OA=![]() (5﹣t),根据OC=
(5﹣t),根据OC=![]() CQ,构建方程即可解决问题;
CQ,构建方程即可解决问题;
(1)在Rt△ABC中,AB=![]() =
=![]() =10,
=10,
BP=2t,AQ=t,则AP=10﹣2t,
∵PQ∥BC,
∴△APQ∽△ABC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得t=![]() ,
,
∴当t=![]() 时,PQ∥BC.
时,PQ∥BC.
(2)过点P作PD⊥AC于D,则有△APD∽△ABC,
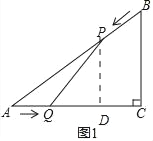
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴PD=6﹣![]() t,
t,
∴y=![]() t(6﹣
t(6﹣![]() t)=﹣
t)=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,y有最大值为
时,y有最大值为![]() .
.
(3)存在.
理由:连接PP′,交AC于点O.
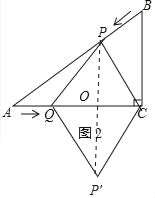
∵四边形PQP′C为菱形,
∴OC=![]() CQ,
CQ,
∵△APO∽△ABC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴OA=![]() (5﹣t),
(5﹣t),
∴8﹣![]() (5﹣t)=
(5﹣t)=![]() (8﹣t),
(8﹣t),
解得t=![]() ,
,
∴当t=![]() 时,四边形PQP′C为菱形.
时,四边形PQP′C为菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
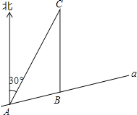
【题目】如图,某市郊景区内一条笔直的公路![]() 经过
经过![]() 、
、![]() 两个景点,景区管委会又开发了风景优美的景点
两个景点,景区管委会又开发了风景优美的景点![]() ,经测量景点
,经测量景点![]() 位于景点
位于景点![]() 的北偏东
的北偏东![]() 方向,位于景点
方向,位于景点![]() 的正北方向,且景点
的正北方向,且景点![]() 位于景点
位于景点![]() 的北偏东
的北偏东![]() 方向,景点
方向,景点![]() 与景点
与景点![]() 距离为
距离为![]() .
.
![]() 求景点
求景点![]() 与景点
与景点![]() 的距离;
的距离;
![]() 为方便游客到景点游玩,景区管委会准备由景点
为方便游客到景点游玩,景区管委会准备由景点![]() 向公路
向公路![]() 修建一条距离最短的公路,不考虑其它因素,求出这条公路的长.(结果保留根号)
修建一条距离最短的公路,不考虑其它因素,求出这条公路的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划建一间多功能数学实验室,将采购两类桌椅:A类是三角形桌,每桌可坐3人,B类是五边形桌,每桌可坐5人.学校拟选择甲、乙两家公司中的一家来采购,两家公司的标价均相同,且规定两类桌椅均只能在同一家公司采购.甲公司对两类桌椅均是以标价出售;乙公司对A类桌椅涨价20%、B类桌椅降价20%出售.经咨询,两家公司给出的数量和费用如下表:
A类桌椅(套) | B类桌椅(套) | 总费用(元) | |
甲公司 | 6 | 5 | 1900 |
乙公司 | 3 | 7 | 1660 |
(1)求第一次购买时,A、B两类桌椅每套的价格分别是多少?
(2)如果该数学实验室需设置48个座位,学校到甲公司采购,应分别采购A、B两类桌椅各多少套时所需费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2018年韶关市开展的“善美韶关情暖三江”的志愿者系列括动中,某志愿者组织筹集了部分资金,计划购买甲、乙两种书包若干个送给贫困山区的学生,已知每个甲种书包的价格比每个乙种书包的价格贵10元,用350元购买甲种书包的个数恰好与用300元购买乙种书包的个数相同,求甲、乙两种书包每个的价格各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
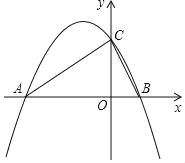
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣4,0),B (1,0)两点,与y轴交于点C.
(1)求这个二次函数的解析式;
(2)连接AC、BC,判断△ABC的形状,并证明;
(3)若点P为二次函数对称轴上点,求出使△PBC周长最小时,点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
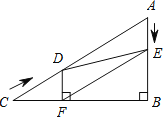
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是反比例函数![]() 上第一象限上一个动点,点A、点B为坐标轴上的点,A(0,k),B(k,0).已知△OAB的面积为
上第一象限上一个动点,点A、点B为坐标轴上的点,A(0,k),B(k,0).已知△OAB的面积为![]() .
.
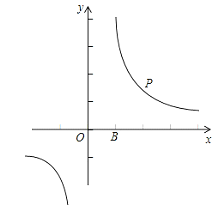
(1)求k的值;
(2)连接PA、PB、AB,设△PAB的面积为S,点P的横坐标为t.请直接写出S与t的函数关系式;
(3)阅读下面的材料回答问题:
当a>0时,![]()
∵![]() ≥0,∴
≥0,∴![]() ≥2,即
≥2,即![]() ≥2
≥2
由此可知:当![]() =0时,即a=1时,
=0时,即a=1时,![]() 取得最小值2.
取得最小值2.
问题:请你根据上述材料探索(2)中△PAB的面积S有没有最小值?若有,请直接写出S的最小值;若没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com