Question

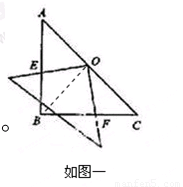
在Rt△ABC中，AB=BC=5，∠B=90°，将一块等腰直角三角板的直角顶点放在斜边AC的中点O处，将三角板绕点O旋转，三角板的两直角边分别交AB，BC或其延长线于E，F两点，如图①与②是旋转三角板所得图形的两种情况．

1.三角板绕点O旋转，△OFC是否能成为等腰直角三角形？若能，指出所有情况（即  

给出△OFC是等腰直角三角形时BF的长）；若不能，请说明理由；

2.三角板绕点O旋转，线段OE和OF之间有什么数量关系？用图①或②加以证明；

3.若将三角板的直角顶点放在斜边上的点P处（如图③），当AP:AC=1:4时，PE和          

          PF有怎样的数量关系？证明你发现的结论．

 

Answer 1

【答案】

 

1.△OFC是能成为等腰直角三角形，

①当F为BC的中点时，

∵O点为AC的中点，AB=BC=5， ∴OF∥AB，    ∴CF=OF=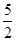，    ∴BF=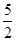

②当B与F重合时，   ∵OF=OC=，     ∴BF=0

2.如图一，连接OB，  ∵由（1）的结论可知，BO=OC=，

∵∠EOB=∠FOC，∠EBO=∠C        ∴△OEB≌△OFC，      ∴OE=OF

3.如图二，过点P作PM⊥AB，PN⊥BC，

∵∠EPM+∠EPN=∠EPN+∠FPN=90°，       ∴∠EPM=∠FPN，

∵∠EMP=∠FNP=90°，       ∴△PNF∽△PME，     ∴PM：PN=PE：PF，

∵△APM和△PNC为等腰直角三角形，      ∴△APM∽△PNC，    ∴PM：PN=AP：PC，

∵PA：AC=1：4，        ∴AP：PC=1：3，     ∴PE：PF=1：3．

【解析】

1.由题意可知，①当F为BC的中点时，由AB=BC=5，可以推出CF和OF的长度，即可推出BF的长度，②当B与F重合时，根据直角三角形的相关性质，即可推出OF的长度，即可推出BF的长度；

2.连接OB，由已知条件推出△OEB≌△OFC，即可推出OE=OF；

3.过点P做PM⊥AB，PN⊥BC，结合图形推出△PNF∽△PME，△APM∽△PNC，继而推出PM：PN=PE：PF，PM：PN=AP：PC，根据已知条件即可推出PA：AC=PE：PF=1：4．