
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,2),B(0,-2)其对称轴为直线x=![]() ,C(0,
,C(0, ![]() )为y轴上一点,直线AC与抛物线交于另一点D,
)为y轴上一点,直线AC与抛物线交于另一点D,
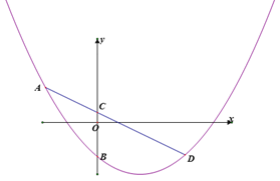
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点F使△ADF是直角三角形,如果存在,求出点F的坐标,如果不存在,请说明理由.
【答案】(1)y=![]() x2-
x2-![]() x-2 ;(2)存在.F点坐标为(
x-2 ;(2)存在.F点坐标为(![]() ,13),(
,13),(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ),(
),(![]() ,-7).
,-7).
【解析】
(1)根据待定系数法求解即可;
(2)先利用待定系数法求出直线AC的解析式,再和抛物线的解析式联立组成方程组求出点D的坐标,设F(![]() ,m),然后根据两点间的距离公式分别表示出AD2、AF2、DF2,再分三种情况根据勾股定理列出方程,解方程即可求得结果.
,m),然后根据两点间的距离公式分别表示出AD2、AF2、DF2,再分三种情况根据勾股定理列出方程,解方程即可求得结果.
解:(1)由题意得: ,解得
,解得 ,
,
∴抛物线的解析式为y=![]() x2-
x2-![]() x-2 ;
x-2 ;
(2)存在点F使△ADF是直角三角形.
设直线AC的解析式为:![]() ,把A(-3,2)、C(0,
,把A(-3,2)、C(0,![]() )代入,得
)代入,得 ,解得:
,解得: ,∴直线AC的解析式为:
,∴直线AC的解析式为:![]() ,
,
联立方程组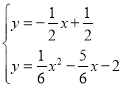 ,解得:
,解得: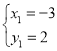 ,
, ,∴点D坐标为(5,-2),
,∴点D坐标为(5,-2),
设F(![]() ,m),AD2=(5+3)2+(-2-2)2=80,AF2=(
,m),AD2=(5+3)2+(-2-2)2=80,AF2=(![]() +3)2+(m-2)2,DF2=(5-
+3)2+(m-2)2,DF2=(5-![]() )2+(m+2)2,
)2+(m+2)2,
当AD2+DF2=AF2时,△ADF是直角三角形,则80+(5-![]() )2+(m+2)2=(
)2+(m+2)2=(![]() +3)2+(m-2)2,
+3)2+(m-2)2,
解得m=-7,此时F点坐标为(![]() ,-7);
,-7);
当DF2+AF2=AD2时,△ADF是直角三角形,则(5-![]() )2+(m+2)2+(
)2+(m+2)2+(![]() +3)2+(m-2)2=80,
+3)2+(m-2)2=80,
解得m=±![]() ,∴F点坐标为(
,∴F点坐标为(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() );
);
当AD2+AF2=DF2时,△ADF也是直角三角形,则80+(![]() +3)2+(m-2)2=(5-
+3)2+(m-2)2=(5-![]() )2+(m+2)2,
)2+(m+2)2,
解得:m=13,∴F点坐标为(![]() ,13).
,13).
综上,在抛物线的对称轴上存在点F,使△ADF是直角三角形,且F点坐标为(![]() ,13)或(
,13)或(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() )或(
)或(![]() ,-7).
,-7).


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
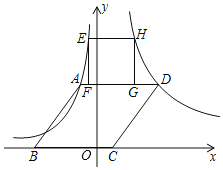
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点B,C在x轴上,反比例函数y=﹣![]() (x<0)的图象经过A,E两点,反比例函数y=
(x<0)的图象经过A,E两点,反比例函数y=![]() (x>0)的图象经过第一象限内的D,H两点,正方形EFCH的顶点F.G在AD上.已知A(﹣1,a),B(﹣4,0).
(x>0)的图象经过第一象限内的D,H两点,正方形EFCH的顶点F.G在AD上.已知A(﹣1,a),B(﹣4,0).
(1)求点C的坐标及k的值;
(2)直接写出正方形EFGH的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,与过
,与过![]() 点的直线相交于另一点
点的直线相交于另一点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .
.

(1)求抛物线的解析式.
(2)点![]() 是
是![]() 轴正半轴上的一个动点,过点
轴正半轴上的一个动点,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
①若点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
②设![]() 的长为
的长为![]() ,是否存在
,是否存在![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为4,点E, F分别在BC, BD上,且BE=1,过三点C, E, F作⊙O交CD于点G.

(1)证明∠EFG =90°.
(2)如图2,连结AF,当点F运动至点A,F, G三点共线时,求![]() 的面积.
的面积.
(3)在点F整个运动过程中,
①当EF, FG, CG中满足某两条线段相等,求所有满足条件的BF的长.
②连接EG,若![]() 时,求⊙O的半径(请直接写出答案) .
时,求⊙O的半径(请直接写出答案) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AM为BC边的中线,点D在边AC上,联结BD交AM于点F,延长BD至点E,使得![]() =
=![]() ,联结CE.
,联结CE.
求证:(1)∠ECD=2∠BAM;
(2)BF是DF和EF的比例中项.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在向贫困地区捐书活动中全体师生积极捐书.为了解所捐书籍的种类,某同学对部分书籍进行了抽样调查,并根据调查数据绘制了如图所示不完整统计图.请根据统计图回答下面问题:

(1)本次抽样调查的书籍有多少本?请通过计算补全条形统计图;
(2)求出图![]() 中表示科普类书籍的扇形圆心角度数;
中表示科普类书籍的扇形圆心角度数;
(3)本次活动师生共捐书![]() 本,请估计有多少本文学类书籍?
本,请估计有多少本文学类书籍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中有2个白球、1个红球,乙口袋中有1个白球、1个红球,这些球除颜色外无其他差别.分别从每个口袋中随机摸出1个球.
(1)求摸出的2个球都是白球的概率.
(2)请比较①摸出的2个球颜色相同②摸出的2个球中至少有1个白球,这两种情况哪个概率大,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).
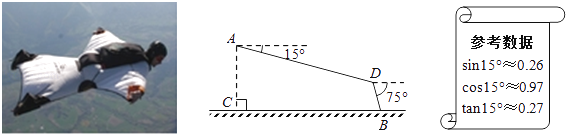
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com