练习册

  • 练习册
  • 试题
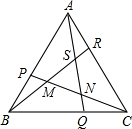    精英家教网 > 初中数学 > 题目详情
    如图，设△ABC为正三角形，边长为1，P，Q，R分别在AB，BC，AC边上，且AR=BP=CQ=
    13
    ．连A精英家教网Q，BR，CP两两相交得到△MNS，则△MNS的面积是
     
    ．
    分析：先根据△ABC为正三角形，边长为1，且AR=BP=CQ=
    1
    3
    得出△BPC≌△COA≌△ARB，△BPC∽△NQC，再求出△BPC及△ABC的面积，由相似三角形的性质可求出△NOC的面积，进而可得出答案．
    解答：解：∵△ABC为正三角形，边长为1，
    ∴S△ABC=
    1
    2
    ×1×
    		3
    2
    =
    		3
    4
    ；精英家教网
    ∵AR=BP=CQ=
    1
    3
    ，
    ∴△BPC≌△COA≌△ARB，
    ∴∠CON=∠BPC，∠BCP=∠BCP，
    ∴△BPC∽△QNC，其相似比为
    QC
    BC
    =
    1
    3
    1
    =
    1
    3
    ，
    ∵S△BPC=
    1
    2
    ×
    1
    3
    ×
    		3
    2
    =
    		3
    12
    ，
    ∴S△BPC=
    		3
    108
    ，
    ∴△MNS的面积=S△ABC-3S△BPC+3S△BPC=
    		3
    4
    -3×
    		3
    12
    +3×
    		3
    108
    =
    		3
    36
    ．
    故答案为：
    		3
    36
    ．
    点评：本题考查的是面积及等积变换，能根据题意得出△BPC∽△NQC，再由相似三角形的性质得出答案是解答此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

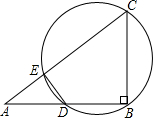    精英家教网（在下面的（I）（II）两题中选做一题，若两题都做，按第（I）题评分）
    （I）如图，在△ABC中，AB=4，BC=3，∠B=90°，点D在AB上运动，但与A、B不重合，过B、C、D三点的圆交AC于E，连接DE．
    （1）设AD=x，CE=y，求y与x之间的函数关系式，并指出自变量x的取值范围；
    （2）当AD长为关于x的方程2x2+（4m+1）x+2m=0的一个整数根时，求m的值．

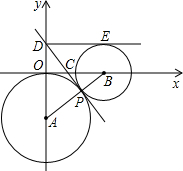    （II）如图，在直角坐标系xOy中，以点A（0，-3）为圆心作圆与x轴相切，⊙B与⊙A外切干点P，B点在x轴正半轴精英家教网上，过P点作两圆的公切线DP交y轴于D，交x轴于C，
    （1）设⊙A的半径为r1，⊙B的半径为r2，且r2=
    23
    r1，求公切线DP的长及直线DP的函数解析式，
    （2）若⊙A的位置、大小不变，点B在X轴正半轴上移动，⊙B与⊙A始终外切．过D作⊙B的切线DE，E为切点．当DE=4时，B点在什么位置？从解答中能发现什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•桥东区二模）如图，Rt△ABC在平面直角坐标系中，BC在x轴上，B（-1，0）、A（0，2），AC⊥AB．
    （1）求线段OC的长．
    （2）点P从B点出发以每秒4个单位的速度沿x轴正半轴运动，点Q从A点出发沿线段AC以
    		5
    个单位每秒速度向点C运动，当一点停止运动，另一点也随之停止，设△CPQ的面积为S，两点同时运动，运动的时间为t秒，求S与t之间关系式，并写出自变量取值范围．
    （3）Q点沿射线AC按原速度运动，⊙G过A、B、Q三点，是否有这样的t值使点P在⊙G上？如果有求t值，如果没有说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=
    1
    2
    ．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．
    根据上述对角的正对定义，解下列问题：
    （1）填空：sad60°=
    1
    1
    ，sad90°=
    		2
    		2
    ，sad120°=
    		3
    		3
    ；
    （2）对于0°＜A＜180°，∠A的正对值sadA的取值范围是
    0＜sadA＜2
    0＜sadA＜2
    ；
    （3）如图，已知sinA=
    3
    5
    ，其中A为锐角，试求sadA的值；
    （4）设sinA=k，请直接用k的代数式表示sadA的值为
    		2-2
    		1-k2
    ．
    		2-2
    		1-k2
    ．
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    （2012•青岛模拟）同学们已经认识了很多正多边形，现以正六边形为例再介绍与正多边形相关的几个概念．如正六边形ABCDEF各边对称轴的交点O，又称正六边形的中心，其中OA称正六边形的半径，通常用R表示，∠AOB称为中心角，显然．提出问题：正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系？
    探索发现：
    （1）为了解决这个问题，我们不妨从最简单的正多边形--正三角形入手．
    如图①，△ABC是正三角形，半径OA=R，∠AOB是中心角，P是△ABC内任意一点，P到△ABC各边距离分别为h1、h2、h3 ，确定h1+h2+h3的值与△ABC的半径R及中心角的关系．
    解：设△ABC的边长是a，面积为S，显然S=
    1
    2
    a（h1+h2+h3）
    O为△ABC的中心，连接OA、OB、OC，它们将△ABC分成三个全等的等腰三角形，过点O作OM⊥AB，垂足为M，Rt△AOM中，易知
    OM=OAcos∠AOM=Rcos
    1
    2
    ∠AOB=Rcos
    1
    2
    ×120°=Rcos60°，
    AM=OAsin∠AOM=Rsin
    1
    2
    ∠AOB=Rsin
    1
    2
    ×120°=Rcos60°
    ∴AB=a=2AM=2Rsin60°
    ∴S△AOB=
    1
    2
    AB×OM=
    1
    2
    ×2Rsin60°•Rcos60°=R2sin60°cos60°
    ∴S△ABC=3S△AOB=3R2sin60°cos60°
    ∴
    1
    2
    a（h1+h2+h3）=3R2sin60°cos60°
    即：
    1
    2
    ×2Rsin60°（h1+h2+h3）=3R2sin60°cos60°
    ∴h1+h2+h3=3Rcos60°
    （2）如图②，五边形ABCDE是正五边形，半径是R，P是正五边形ABCDE内任意一点，P到五边形ABCDE各边距离分别为h1、h2、h3、h4、h5，参照（1）的探索过程，确定h1+h2+h3+h4+h5的值与正五边形ABCDE的半径R及中心角的关系．
    （3）类比上述探索过程，直接填写结论
    正六边形（半径是R）内任意一点P到各边距离之和 h1+h2+h3+h4+h5+h6=
    6Rcos30°
    6Rcos30°

    正八边形（半径是R）内任意一点P到各边距离之和 h1+h2+h3+h4+h5+h6+h7+h8=
    8Rcos22.5°
    8Rcos22.5°

    正n边形（半径是R）内任意一点P到各边距离之和  h1+h2+…+hn=
    nRcos
    180°
    n
    nRcos
    180°
    n
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，边长均为6的正△ABC和正△A′B′C′原来完全重合．如图2，现保持正△ABC不动，使正△A′B′C′绕两个正三角形的公共中心点O按顺时针方向旋转，设旋转角度为α（α＞0°）．（注：除第 （3）题中的第②问，其余各问只要直接给出结果即可）
    （1）当α多少时，正△A′B′C′与正△ABC出现旋转过程中的第一次完全重合？
    （2）当0°＜α＜360°时，要使正△A′B′C′与正△ABC重叠部分面积最小，α可以取哪些角度？
    （3）旋转时，如图3，正△ABC和正△A′B′C′始终具有公共的外接圆⊙O．当0°＜α＜60°时，记正△A′B′C′与正△ABC重叠部分为六边形DEFGHI．当α在这个范围内变化时，
    ①求△ADI面积S相应的变化范围；
    ②△ADI的周长是否一定？说出你的理由．
    精英家教网

    查看答案和解析>>

    同步练习册答案