
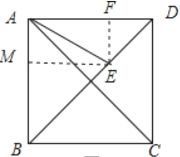
【题目】如图,在正方形ABCD中,点E为对角线BD上一动点.若AB=![]() ,当∠EAC=15°时,线段BE的长度为_________.
,当∠EAC=15°时,线段BE的长度为_________.

【答案】![]() 或
或![]()
【解析】
分两种情况:当点E在近D点时,过E作EF⊥AD于F,EM⊥AB于M,由∠CAE=15°,得出∠DAE=45°-15°=30°,设EF=x,则DF=x,AF=![]() x,根据AD-AF=DF得出
x,根据AD-AF=DF得出![]() +1-
+1-![]() x=x,从而求出EF、AM、AE的长,然后根据勾股定理求得ME的值,进而求出BE的长;当点E近B点时,同理可求BE的长.
x=x,从而求出EF、AM、AE的长,然后根据勾股定理求得ME的值,进而求出BE的长;当点E近B点时,同理可求BE的长.
解:当点E在近D点时,
过E作EF⊥AD于F,EM⊥AB于M,
∴四边形AMEF是矩形,
∵∠CAE=15°,
∴∠DAE=45°-15°=30°,
设EF=x,则DF=x,AF=![]() x,
x,
∵AD-AF=DF
∴![]() +1-
+1-![]() x=x,
x=x,
解得x=1
∴EF=AM=1
∴AF=MB=BM=![]() ,
,
∴BE=![]() =
=![]()
同理,当点E在近B点时,可得BE=![]() .
.
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】同学们,我们很熟悉这样的算式:![]() ,其实,数学不仅非常美妙,而且魅力无穷.请你欣赏下列一组等式:
,其实,数学不仅非常美妙,而且魅力无穷.请你欣赏下列一组等式:
①![]()
②![]()
③![]()
④![]()
⑤……
(1)写出第⑤个等式:![]()
(2)根据上述规律,写出第![]() 个等式:
个等式:
![]()
(3)观察比较,并大胆猜想:
![]()
(4)根据(2)的规律计算![]() (写出计算过程)
(写出计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG= ![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的义务植树活动中,甲、乙两组各四名同学的植树棵数如下,甲组:9,9,11,10;乙组:9,8,9,10;分别从甲、乙两组中随机选取一名同学,则这两名同学的植树总棵数为19的概率 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四个命题:
①对应角和面积都相等的两个三角形全等;
②“若x2﹣x=0,则x=0”的逆命题;
③若关于x、y的方程组 ![]() 有无数多组解,则a=b=1;
有无数多组解,则a=b=1;
④将多项式5xy+3y﹣2x2y因式分解,其结果为﹣y(2x+1)(x﹣3).
其中正确的命题的序号为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140 146 143 175 125 164 134 155 152 168 162 148
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据中位数,推断他的成绩如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有三个小球,小球上分别标有数字﹣1、0、2,它们除了数字不同外,其他都完全相同.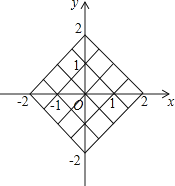
(1)随机地从布袋中摸出一个小球,则摸出的球为标有数字2的小球的概率为;
(2)小丽先从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点M的横坐标.再将此球放回、搅匀,然后由小华再从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点M的纵坐标,请用树状图或表格列出点M所有可能的坐标,并求出点M落在如图所示的正方形网格内(包括边界)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com