
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正确的结论的有__________.(把正确结论的序号都写上去)

【答案】①②③
【解析】
根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,结合题中所给结论逐步推理,即可判断各项.
解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正确;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
∴∠ACB=2∠ADB,∴②正确;
∵AD平分∠EAC,CD平分∠ACF,
∴∠DAC=![]() ∠EAC,∠DCA=
∠EAC,∠DCA=![]() ∠ACF,
∠ACF,
∵∠EAC=∠ACB+∠ABC,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC=180°,
∴∠ADC=180°(∠DAC+∠ACD)
=180°![]() (∠EAC+∠ACF)
(∠EAC+∠ACF)
=180°![]() (∠ABC+∠ACB+∠ABC+∠BAC)
(∠ABC+∠ACB+∠ABC+∠BAC)
=180°![]() (180°+∠ABC)
(180°+∠ABC)
=90°![]() ∠ABC
∠ABC
=90°﹣∠ABD,∴③正确;
∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,
∴∠BAC=2∠BDC,∴④错误;
故答案为:①②③.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知平面直角坐标系内A(2a-1,4),B(-3,3b+1),A、B两点关于y轴对称。
(1)求A、B的坐标
(2)动点P、Q分别从A点、B点同时出发,沿直线AB向右运动,同向而行,P点的速度是每秒2个单位长度,Q点的速度是每秒4个单位长度,设P、Q的运动时间为t秒,当0<t<3时.
①请用含t的代数式表示三角形OPQ的面积S,
②在平面直角坐标系中存在一点M,点M的横纵坐标相等,且满足![]() ,求出点M的坐标,并求出当
,求出点M的坐标,并求出当![]() =15时,三角形OPQ的面积.
=15时,三角形OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16km,一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此时货轮与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,![]() ≈1.41,
≈1.41,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同.
(1)求这种笔和本子的单价;
(2)该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(-1,y1),(2,y2),(3,y3)在反比例函数![]() 的图象上.下列结论中正确的是( )
的图象上.下列结论中正确的是( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y1>y2 D. y2>y3>y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘一辆检修车沿铁路检修,规定向东走为正,向西走为负,该小组的出发地记为A,某天检修完毕时,行走记录(单位.千米)如下.
+10,-2,+3,-1,+5,-3,-2,+11,+3,-4,+6.
(1)问收工时,检修小组距出发地有多远?在东侧还是西侧?
(2)距离A最近的一次是哪一次?距离多远?
(3)若检修车每千米耗油2.8升,求从出发到收工共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
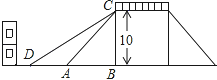
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=![]() :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 的顶点为A.
的顶点为A.
(1)求点A的坐标;

(2)将线段![]() 沿
沿![]() 轴向右平移2个单位得到线段
轴向右平移2个单位得到线段![]() .
.
①直接写出点![]() 和
和![]() 的坐标;
的坐标;
②若抛物线![]() 与四边形
与四边形![]() 有且只有两个公共点,结合函数的图象,求
有且只有两个公共点,结合函数的图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com