
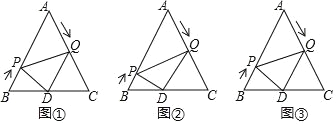
����Ŀ����ͼ����֪��ABC�DZ߳�Ϊ6cm�ĵȱ������Σ�����P��Qͬʱ��B��A����������ֱ���BA��AC�����˶������е�P�˶����ٶ���1cm/s����Q�˶����ٶ���2cm/s������Q�����Cʱ��P��Q���㶼ֹͣ�˶������˶�ʱ��Ϊt��s��������������⣺
��1����ͼ�٣���tΪ��ֵʱ��AP��3AQ��
��2����ͼ�ڣ���tΪ��ֵʱ����APQΪֱ�������Σ�
��3����ͼ�ۣ��� QD��AB�� BC�ڵ�D������PD����tΪ��ֵʱ����BDP���PDQ���ƣ�
���𰸡���1��![]() ��2��3��
��2��3��![]() ��3��
��3��![]() ��2
��2
��������
(1)�������֪BP=t,AQ=2t,��AP=6-t��AP=3AQ�ɵõ�����t�ķ���,����õ�ֵ;
(2)�֡�APQ=90![]() �ͦ�AQP=90
�ͦ�AQP=90![]() �������,�����ú�30�ǵ�ֱ�������ε����ʿɺ�AP=2AQ,��AQ=2AP,�ֱ���;
�������,�����ú�30�ǵ�ֱ�������ε����ʿɺ�AP=2AQ,��AQ=2AP,�ֱ���;
(3) ����֪��֤�á�CDQ �ǵȱ������Σ��֡�BPD�ס�PDQ ����BPQ �ס�QDP ����������ۣ��ɵ�t��ֵ.
��1��������֪��AQ��2t��BP��t��
�ߡ�ABC �DZ߳�Ϊ 6cm �ĵȱ������Σ�
���A��60�㣬AB��6��
��AP��AB��BP��6��t��
��AP��3AQ��
��6��t��3��2t��
��t��![]() ��
��
����t��![]() ��ʱ��AP��3AQ��
��ʱ��AP��3AQ��
��2���ɣ�1��֪����A��60�㣬AQ��2t��AP��6��t��
�ߡ�APQ Ϊֱ�������Σ�
�ٵ���APQ��90��ʱ��AQ��2AP��
��2t��2��6��t����
��t��3 �룬
�ڵ���AQP��90��ʱ��AP��2AQ��
��6��t��2��2t��
��t��![]() �룬
�룬
����t��3 ���![]() ��ʱ����APQ ��ֱ�������Σ�
��ʱ����APQ ��ֱ�������Σ�
��3��������֪��AQ��2t��BP��t��
��AP��6��t��
�ߡ�ABC �ǵȱ������Σ�
���A����C��60�㣬
��QD��AB��
���PDQ����BPD����QDB����A��60�㣬
���CDQ �ǵȱ������Σ�
��CD��CQ��
��BD��AQ��2t��
�ߡ�BDP ���PDQ ���ƣ�
��ٵ���BPD�ס�PDQ ʱ��
���B����DPQ��60�㣬
���APQ����BDP��
�ߡ�A����B��
���APQ�ס�BDP��
��![]() ��
��
��![]() ��
��
��t��![]() �룬
�룬
�ڵ���BPQ �ס�QDP ʱ��
���B����DQP��60�㣬
��DQ��AB��
���APQ��DQP��60�㣬
�ߡ�A��60�㣬
���APQ �ǵȱ������Σ�
��AP��AQ��
��6��t��2t��
��t��2 �룬
����t��![]() ��� 2 ��ʱ����BDP ���PDQ ���ƣ�
��� 2 ��ʱ����BDP ���PDQ ���ƣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �ĶԽ���
�ĶԽ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ��
��
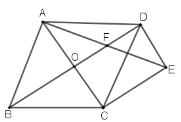
��1����֤�ı���![]() Ϊ����
����
��2����![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳
С����С����ͬ̽��һ����ѧ�⣺
��ͼ�٣��ڡ�ABC�У���D�DZ�BC���е㣬��BAD=65�㣬��DAC=50�㣬AD=2��
��AC��
̽������
С����˼·�ǣ��ӳ�AD����E��ʹDE=AD������ȫ�������Σ�
С����˼·�ǣ�����C��CE��AB����AD���ӳ����ڵ�E������ȫ�������Σ�
ѡ��С����С������һ�˵ķ�����������龳�е����⣮
���Ӧ��
��ͼ�ڣ����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����O��BD���е㣬
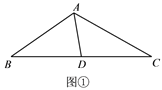

AB��AC������CAD=45�㣬��ADC=67.5�㣬AO=2����BC�ij�Ϊ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC �У� ![]() ��D��E��б��BC�����㣬����DAE=45��������
��D��E��б��BC�����㣬����DAE=45��������![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת90
˳ʱ����ת90![]() �õ���
�õ���![]() ������
������![]() .�н��ۣ�
.�н��ۣ�
�١�ADC�ա�AFB���ڡ� ![]() �ա�
�ա�![]() ���ۡ�
���ۡ�![]() �ա�
�ա�![]() ����
����![]()
������ȷ����( )

A. �ڢ� B. �٢� C. �ڢ� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��У����ȫ�ǽ���������ע���ȵ����⣬��ȫ������Ҫ�dz��ٺͳ��أ�ij��ѧ���꼶��ѧ�С������˲��������ٶȵ�ʵ�飬��ͼ�����ڱ�ֱ�Ĺ�·l��ѡȡһ��A���ڹ�·l��ȷ����B��C��ʹ��AC��l����BAC=60��������AC��ȷ����D��ʹ����BDC=75�㣬���AD=40������֪��·�ζ�У��������50ǧ��/ʱ�������ijУ����B��C������ʻ��ʱ10�룬���������ڱ�·���Ƿ��٣���˵�����ɣ��ο����ݣ�![]() =1.41��
=1.41��![]() =1.73��
=1.73��
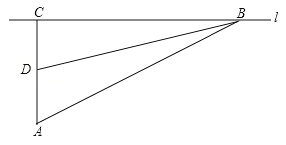
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
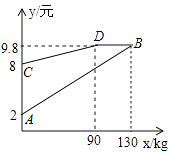
����Ŀ��2015��ȫ������Ѳ���ԼΪ4200��֣���2014������2.1%��ij��ҵ�ӹ������ۿ����ѣ�������������ӹ�����ȣ���ͼ�У��߶�AB������CDB�ֱ��ʾ������ÿǧ�˵ļӹ��ɱ�y1��Ԫ�������ۼ�y2��Ԫ�������x��kg��֮��ĺ�����ϵ��
��1���������ͼ�е�B�ĺ����ꡢ�������ʵ�����壻
��2�����߶�AB����ʾ��y1��x֮��ĺ�������ʽ��
��3����0��x��90ʱ����ÿ����ѵIJ���Ϊ����ʱ������ҵ��õ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
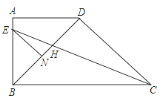
����Ŀ����ͼ����ֱ������ABCD�У�AD��BC����ABC=90�㣬BD��DC��BD=DC��CEƽ����BCD����AB�ڵ�E����BD�ڵ�H��EN��DC��BD�ڵ�N�����н��ۣ�
��BH=DH����CH=(![]() +1)EH����
+1)EH����![]() ��
��![]() �� ������ȷ���ǣ�������
�� ������ȷ���ǣ�������
A. �٢� B. �ڢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
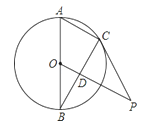
����Ŀ����ͼ��ABΪ��O��ֱ����DΪ��BC�����ģ�����OD���ӳ�������C�������ڵ�P������AC����֤����CPD�ס�ABC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
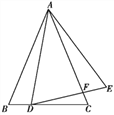
����Ŀ����ͼ,�ڡ�ABC��,AB=AC,��D�ڱ�BC��,����AD,���߶�AD�Ƶ�A��ʱ����ת��AE,ʹ�á�DAE=��BAC,����DE��AC��F,��д��ͼ��һ�����Ƶ�������:____(ֻҪд��һ�Լ���).
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com