
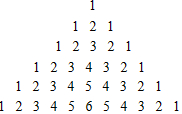
分析 (1)从第1行开始找规律:确定第n行:第n个数和第n+1个数;总结规律即可;
(2)根据数表:每一行中间的数最大,依次向前减1;所以要分情况进行讨论:
①当m≤n时,即为中间前面的数,第几个数就是几;
②当m>n时,即中间后面的数,依次小1,每个数为2n-m;
(3)从k=1开始依次计算:从第1行到第n行这n行中所有等于k的数之和,并找规律即可,
解答 解:(1)第1行:第1个数为1;
第2行:第2个数为2,第3个数为2-1=1;
第3行:第3个数为3,第4个数为3-1=2;
第4行:第4个数为4,第5个数为4-1=3;
…
第8行:第8个数为8,第9个数为8-1=7,
第8行各数的和=1+2+3+…+8+7+…+1=64;
故答案为:7;64;
(2)分两种情况:
①当m≤n时,a=m;
②当m>n时,a=2n-m;
(3)当k=1时,从第1行到第n行这n行中所有等于1的数之和=1×(2n-1)=2n-1.
当k=2时,从第1行到第n行这n行中所有等于k的数之和=2×[2(n-1)-1]=4n-6.
当k=3时,从第1行到第n行这n行中所有等于k的数之和=3×[2(n-2)-1]=6n-15.
…
∴若正整数k≤n.从第1行到第n行这n行中所有等于k的数之和=k[2n-(2k-1)]=2nk-2k2+k.
点评 本题考查了数字的变化类,解题的关键是通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题.


科目:初中数学 来源: 题型:选择题
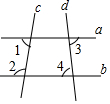 如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4度数是( )
如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4度数是( )| A. | 80° | B. | 85° | C. | 95° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com