解:如图,

∵AE是∠CAB的平分线,DE是∠CDB的平分线,
∴∠1=∠2,∠3=∠4,
在△AEQ和△DBQ,有∠2+∠E=∠4+∠B①,
在△ACP和△DBP,有∠1+∠2+∠C=∠3+∠4+∠B,即2∠2+∠C=2∠4+∠B②,
由①×2-②得,2∠E-∠C=∠B,
又∵∠C=40°,∠E=35°,
∴∠B=2×35°-40°=30°.
所以∠B的度数为30°.
分析:由AE是∠CAB的平分线,DE是∠CDB的平分线,得到∠1=∠2,∠3=∠4,根据三角形的内角和定理得:在△AEQ和△DBQ,有∠2+∠E=∠4+∠B①,在△ACP和△DBP,有∠1+∠2+∠C=∠3+∠4+∠B,即2∠2+∠C=2∠4+∠B②,则由①×2-②得,2∠E-∠C=∠B,已知∠C=40°,∠E=35°,即可求出∠B的度数.
点评:本题考查了三角形的内角和定理:三角形的三个内角的和为180°.也考查了角平分线性质.

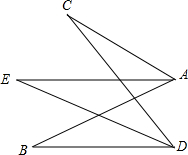 如图AE是∠CAB的平分线,DE是∠CDB的平分线,∠C=40°,∠E=35°.求∠B的度数.
如图AE是∠CAB的平分线,DE是∠CDB的平分线,∠C=40°,∠E=35°.求∠B的度数.

