
分析 (1)根据方程有实数根可得出△≥0,求出k的取值范围即可;
(2)把x=1代入,求出k的值即可;
(3)根据根与系数的关系得出m的表达式,进而可得出结论.
解答 解:(1)∵一元二次方程且x2-2(k-3)x+k2-4k-1=0有实根,
∴△≥0,即△=[-2(k-3)]2-4(k2-4k-1)≥0,解得k≤$\frac{13}{2}$;
(2)∵这方程有一个根为1,
∴12-2(k-3)+k2-4k-1=0,解得k=3±$\sqrt{3}$;
(3)设方程的两根分别为x1,x2,则x1x2=k2-4k-1,
∵方程的两根为横、纵坐标的点恰好在反比例函数y=$\frac{m}{x}$的图象上,
∴m=x1x2=k2-4k-1,
∴m最小=$\frac{-4-16}{4}$=-5.
点评 本题主要考查了根的判别式、一元二次方程的解以及反比例函数图象上点的坐标特征的知识,熟知根与系数的关系是解答此题的关键.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
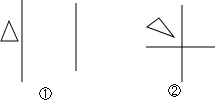 如图,请画出一个图形经过两次轴对称变换之后得到的图形,其中图①中的两条对称轴是平行的,图②中的两条对称轴是垂直的.仔细观察上面的两个图形经过两次轴对称变换之后得到的图形.图①中的图形除经过两次轴对称变换得到之外,还可以通过我们学过的平移变换得到,图②中的图形还可以通过旋转变换得到.
如图,请画出一个图形经过两次轴对称变换之后得到的图形,其中图①中的两条对称轴是平行的,图②中的两条对称轴是垂直的.仔细观察上面的两个图形经过两次轴对称变换之后得到的图形.图①中的图形除经过两次轴对称变换得到之外,还可以通过我们学过的平移变换得到,图②中的图形还可以通过旋转变换得到.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com