练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．直线AB，CD相交于点O，OE平分∠BOC．
    （1）如图1，若∠BOE=25°，求∠AOD的度数．
    （2）如图2，作OF平分∠AOE，若∠FOC=45°，求∠AOD的度数．

    分析 （1）根据角平分线的定义得出∠BOC的度数，再利用对顶角解答即可．
    （2）设∠COE为x，根据角平分线的定义解答即可．

    解答 解：（1）∵OE平分∠BOC，∠BOE=25°，
    ∴∠BOC=50°，
    ∴∠AOD=50°，
    （2）设∠COE为x，
    ∵OE平分∠BOC，OF平分∠AOE，∠FOC=45°，
    可得：2（x+45°）+x=180°
    解得：x=30°，
    ∴∠AOD=∠BOC=60°．

    点评 本题考查了对顶角与邻补角，利用了对顶角的性质，角平分线的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．如图，O为直线AB上一点，已知∠AOC=50°，OD平分∠AOC，OE评分∠BOC．
    （1）求∠DOE的度数；
    （2）求∠BOE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

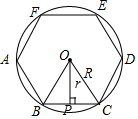    14．三正多边形的中心、半径、中心角、弦心距、边长之间的关系如图：请指出圆内接正六边形的中心、半径、中心角、弦心距．若设半径为R、弦心距为r，边长为a，则R、r、a之间有怎么的数量关系？周长、面积？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知，如图∠1和∠2是直线a，b被直线c截出的内错角，且∠1=∠2，求证：a∥b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图所示，四边形ABCD是一个边长为90米的正方形，甲在A处，乙在B处，两人同时出发，都沿A→B→C→D→A…的方向行走，甲每分钟走65米，乙每分钟走72米，则两人第一次相遇在正方形的哪条边上？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

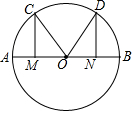    8．如图，已知AB为圆O的直径，M，N分别为OA，OB的中点，CM⊥AB，DN⊥AB，垂足分别为M，N，连结OC，OD，求证：$\widehat{AC}$=$\widehat{BD}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．阅读下面计算过程：
    $\frac{1}{\sqrt{2}+1}$=$\frac{1×（\sqrt{2}-1）}{（\sqrt{2}+1）（\sqrt{2}-1）}$=$\sqrt{2}$-1；
    $\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×（\sqrt{3}-\sqrt{2}）}{（\sqrt{3}+\sqrt{2}）（\sqrt{3}-\sqrt{2}）}$=$\sqrt{3}$-$\sqrt{2}$；
    $\frac{1}{\sqrt{5}+2}$=$\frac{1×（\sqrt{5}-2）}{（\sqrt{5}+2）（\sqrt{5}-2）}$=$\sqrt{5}$-2．
    求：（1）$\frac{1}{\sqrt{7}+\sqrt{6}}$的值．
    （2）$\frac{1}{\sqrt{n+1}+\sqrt{n}}$（n为正整数）的值．
    （3）$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{100}+\sqrt{99}}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

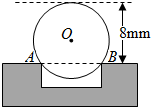    12．工程上常用钢珠来测量零件上小圆孔的宽口，假设钢珠的直径是10mm，测得钢珠顶端离零件表面的距离为8mm，如图所示．
    （1）用尺规作图确定这个圆孔的圆心位置；（不写作法，保留作图痕迹）
    （2）求这个小圆孔的宽口AB的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图为某工艺品摆件，此摆件可以看做是由长方体书本一角插入水平桌面的空隙EF组成．摆件的主视图是矩形ABCD．经测量，AB=18cm，BC=24cm，EF=10cm．
    （1）如图1，若AB=AE，则CF=EF吗？说明理由；
    （2）如图2，若∠DEF=60°，求点B到水平桌面的距离．

    查看答案和解析>>

    同步练习册答案