
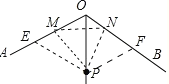
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=3,若点M,N分别在OA,OB上,ΔPMN为等边三角形,则满足上述条件的△PMN有中( )

A. 1个B. 2个C. 3个D. 3个以上
【答案】D
【解析】
首先在OA、OB上截取OE=OF=OP,作∠MPN=60°,由OP平分∠AOB,∠EOP=∠POF=60°,OP=OE=OF,判断出△OPE,△OPF是等边三角形,得出EP=OP,∠EPO=∠OEP=∠PON=∠MPN=60°,进而得出∠EPM=∠OPN,再由ASA判定△PEM≌△PON,得出PM=PN,又∠MPN=60°,可知△PNM是等边三角形,因此只要∠MPN=60°,△PMN就是等边三角形,故这样的三角形有无数个.
解:如图在OA、OB上截取OE=OF=OP,作∠MPN=60°
∵OP平分∠AOB,
∴∠EOP=∠POF=60°,
∵OP=OE=OF,
∴△OPE,△OPF是等边三角形,
∴EP=OP,∠EPO=∠OEP=∠PON=∠MPN=60°,
∴∠EPM=∠OPN,
在△PEM和△PON中,
∠PEM=∠PON
PE=PO
∠EPM=∠OPN
∴△PEM≌△PON.
∴PM=PN,
∵∠MPN=60°,
∴△PNM是等边三角形,
∴只要∠MPN=60°,△PMN就是等边三角形,
故这样的三角形有无数个,
故选D


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片ABC(如图甲),其中AB=AC.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意三点
中,对于任意三点![]() ,
,![]() ,
,![]() 给出如下定义:如果矩形的任何一条边均与某条坐标轴平行或共线,且
给出如下定义:如果矩形的任何一条边均与某条坐标轴平行或共线,且![]() ,
,![]() ,
,![]() 三点都在矩形的内部或边界上,那么称该矩形为点
三点都在矩形的内部或边界上,那么称该矩形为点![]() ,
,![]() ,
,![]() 的外延矩形,在点
的外延矩形,在点![]() ,
,![]() ,
,![]() 所有的外延矩形中,面积最小的矩形称为点
所有的外延矩形中,面积最小的矩形称为点![]() ,
,![]() ,
,![]() 的最佳外延矩形.例如,图
的最佳外延矩形.例如,图![]() 中的矩形
中的矩形![]() ,
,![]() ,
,![]() 都是点
都是点![]() ,
,![]() ,
,![]() 的外延矩形,矩形
的外延矩形,矩形![]() 是点
是点![]() ,
,![]() ,
,![]() 的最佳外延矩形.
的最佳外延矩形.
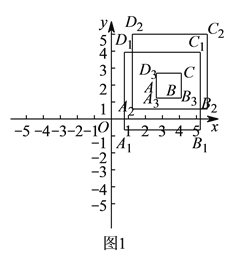
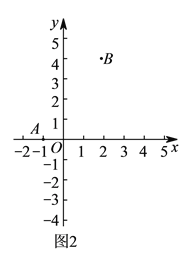
(![]() )如图
)如图![]() ,点
,点![]() ,
,![]() ,
,![]() (
(![]() 为整数).
为整数).
①如果![]() ,则点
,则点![]() ,
,![]() ,
,![]() 的最佳外延矩形的面积是__________.
的最佳外延矩形的面积是__________.
②如果点![]() ,
,![]() ,
,![]() 的最佳外延矩形的面积是
的最佳外延矩形的面积是![]() ,且使点
,且使点![]() 在最佳外延矩形的一边上,请写出一个符合题意的
在最佳外延矩形的一边上,请写出一个符合题意的![]() 值__________.
值__________.
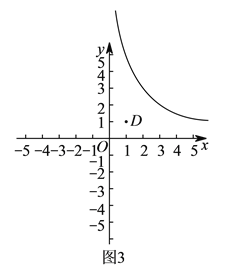
(![]() )如图
)如图![]() ,已知点
,已知点![]() 在函数
在函数![]() 的图象上,且点
的图象上,且点![]() 的坐标为
的坐标为![]() ,求点
,求点![]() ,
,![]() ,
,![]() 的最佳外延矩形的面积
的最佳外延矩形的面积![]() 的取值范围以及该面积最小时
的取值范围以及该面积最小时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂加工某种茶叶,计划一周生产![]() 千克,平均每天生产
千克,平均每天生产![]() 千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(![]() )这一周的实际产量是多少千克?
)这一周的实际产量是多少千克?
(![]() )该厂规定工人工资参照平均产量计发,每千克
)该厂规定工人工资参照平均产量计发,每千克![]() 元.若超产,则超产的部分每千克
元.若超产,则超产的部分每千克![]() 元;若低于平均产量,按实际产量计发,而且每少
元;若低于平均产量,按实际产量计发,而且每少![]() 千克扣除
千克扣除![]() 元,那么该工厂工人这一周的工资总额是多少?
元,那么该工厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,则△ABD的周长是( )

A. 22cmB. 20cmC. 18cmD. 15cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.

(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,CE平分∠ACB,交BD于点E.下列结论:①BD是∠ABC的角平分线;②ΔBCD是等腰三角形;③BE=CD;④ΔAMD≌ΔBCD;⑤图中的等腰三角形有5个。其中正确的结论是___.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
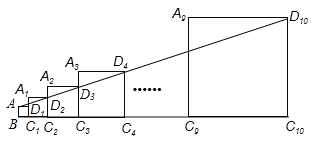
【题目】已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推…,若A1C1=2,且点A,D2, D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据证明过程,在括号内填写相应理由,如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D,
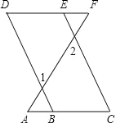
求证:∠A=∠F.
证明:因为∠1=∠2(已知)
所以BD∥CE( )所以∠C=∠ABD( )因为∠C=∠D( )
所以∠D=∠ABD( )
所以DF∥AC( )所以∠A=∠F( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com