
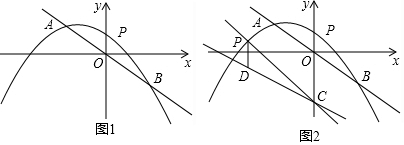
���� ��1���ѵ�A��-3��3������y=kx���k�������B�����꣬��A��-3��3�����������߽���ʽ���c���ɼ������⣮
��2����ͼ1�У�����BM����ֱ��BM�Ľ���ʽΪy=kx+b�����ô���ϵ�������ֱ��BM�Ľ���ʽ����P��m��-$\frac{1}{4}$m2-m+$\frac{9}{4}$����P��PF��x�ύBM�ڵ�F������S�ı���PMAB=S��PBM+S��AMB�������κ������ɽ�����⣮
��3����ͼ2�У��������C��ƽ��ǰ������C�䣨-$\frac{3}{4}$��0������ƽ��ǰ��ֱ�ߵĽ���ʽΪy=-$\frac{3}{4}$x-$\frac{3}{4}$��x�� �Ľ�������G��-1��0���������ƽ�ƺ��ֱ�ߣ�ƽ�ƺ�Ľ���ʽΪy=-$\frac{3}{4}$x-$\frac{23}{4}$����P��t��-$\frac{1}{4}$t2-t+$\frac{9}{4}$������D��t��-$\frac{3}{4}$t-$\frac{23}{4}$������취�г����̼��ɽ�����⣮
��� �⣺��1����A��-3��3����y=kx�ϣ�
��3=-3k��
��k=-1
B��3��b����y=-x�ϣ�
��b=-3
��A��-3��3����y=-$\frac{1}{4}$x2-x+c�ϣ�
��3=-$\frac{1}{4}$����-3��2-��-3��+c��
��c=$\frac{9}{4}$��
�������ߵĽ���ʽΪy=-$\frac{1}{4}$x2-x+$\frac{9}{4}$��
��y=-$\frac{1}{4}$x2-x+$\frac{9}{4}$=-$\frac{1}{4}$��x+2��2+$\frac{13}{4}$��
�ඥ��M��-2��$\frac{13}{4}$����
��2����ͼ1�У�����BM����ֱ��BM�Ľ���ʽΪy=kx+b��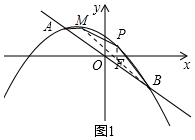
�߾���B��3��-3����M��-2��$\frac{13}{4}$����
��$\left\{\begin{array}{l}{-2k+b=\frac{13}{4}}\\{3k+b=-3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{5}{4}}\\{b=\frac{3}{4}}\end{array}\right.$��
��ֱ��BM�Ľ���ʽΪy=-$\frac{5}{4}$x+$\frac{3}{4}$��
��P��m��-$\frac{1}{4}$m2-m+$\frac{9}{4}$����P��PF��x�ύBM�ڵ�F��
��F��m��-$\frac{5}{4}$m+$\frac{3}{4}$����
��PF=-$\frac{1}{4}$m2-m+$\frac{9}{4}$+$\frac{5}{4}$m-$\frac{3}{4}$=-$\frac{1}{4}$m2+$\frac{1}{4}$m+$\frac{3}{2}$��
��S�ı���PMAB=S��PBM+S��AMB=$\frac{1}{2}$��5����-$\frac{1}{4}$m2+$\frac{1}{4}$m+$\frac{3}{2}$��+$\frac{1}{2}$����$\frac{13}{4}$-2����6
=-$\frac{5}{8}$m2+$\frac{5}{8}$m+$\frac{15}{2}$
=-$\frac{5}{8}$��m-$\frac{1}{2}$��2+$\frac{245}{32}$��
��a=-$\frac{5}{8}$��0��
��m=$\frac{1}{2}$ʱ���ı���PMAB��������ֵΪ$\frac{245}{32}$����ʱP��$\frac{1}{2}$��$\frac{27}{16}$����
��3����ͼ2�У��������C��ƽ��ǰ������C�䣨0��-$\frac{3}{4}$������ƽ��ǰ��ֱ�ߵĽ���ʽΪy=-$\frac{3}{4}$x-$\frac{3}{4}$��x�� �Ľ�������G��-1��0����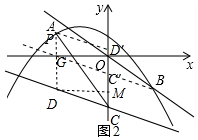
��ƽ�ƺ�Ľ���ʽΪy=-$\frac{3}{4}$x-$\frac{23}{4}$����P��t��-$\frac{1}{4}$t2-t+$\frac{9}{4}$������D��t��-$\frac{3}{4}$t-$\frac{23}{4}$����
��PD=|-$\frac{1}{4}$t2-t+$\frac{9}{4}$+$\frac{3}{4}$t+$\frac{23}{4}$|��
��DM��y����M���ɡ�DMC�ס�GOC�䣬
��$\frac{DM}{GP}$=$\frac{CD}{GC��}$��
��CD=|$\frac{5}{4}$m|��
��D��D�����PC�Գƣ�
���PCD=��PCD��=��DPC��
��PD=DC��
��-$\frac{1}{4}$t2-t+$\frac{9}{4}$+$\frac{3}{4}$t+$\frac{23}{4}$=��$\frac{5}{4}$t��
���t=-3��$\sqrt{41}$��-4��8��
�����������ĵ�P����Ϊ��8��-$\frac{87}{4}$����-4��$\frac{9}{4}$����-3+$\sqrt{41}$��$\frac{\sqrt{41}}{2}$-$\frac{29}{4}$����-3-$\sqrt{41}$��-$\frac{\sqrt{41}}{2}$-$\frac{29}{4}$����
���� ���⿼����κ���������ϵ������һ�κ��������������ε����ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�ṹ�����κ��������ֵ���⣬ѧ���÷��̵�˼��˼�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
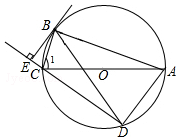 ��ͼ����O�ǡ�ABC�����Բ��ACΪֱ������BD=BA������B����O�����߽�DC���ӳ����ڵ�E��
��ͼ����O�ǡ�ABC�����Բ��ACΪֱ������BD=BA������B����O�����߽�DC���ӳ����ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2a+3b=5ab | B�� | a3•a3•a3=3a3 | C�� | ��ab2��3=a3b6 | D�� | ��a+b��2=a2+b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���������� | B�� | ֱ�������� | C�� | ��������� | D�� | �۽������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12��15��18 | B�� | 12��35��36 | C�� | 0.3��0.4��0.5 | D�� | 5��12��13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | 2 | D�� | -2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com