
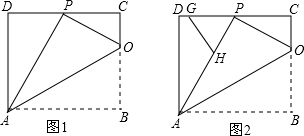
���� ��1���������۵������Լ����ɶ����ɵ�DP��ֵ���ɡ�ADP�ס�PCO��AC��OB��AB��ֵ�������ó���OAB=30�㣬��֤��ADP�ס�APO��
���ɢٿ�֪AB��ֵ��
��2�����ɡ�ADP�ס�PCO����OCP���PDA�������Ϊ1��4���ɵ�DP=2CO��AD=2PC����RT��ADP�У�����AP2=AD2+DP2���ɵ�AB=10��
����GP=6-t��PH=2t�����GPH�ĸ�Ϊh����ɵ�h��ֵ����˲ϢS�ı���ADGH=S��ADP-S��GHP���ɵó���t=3ʱ���ı���ADGH�����S����Сֵ��
��� �⣺��1���١ߵ�Pǡ����CD�ߵ��е㣬
��DP=PC=y��
��DC=AB=AP=2y��
��Rt��ADP��AD2+DP2=AP2��
����82+y2=��2y��2��
��ã�y=$\frac{8\sqrt{3}}{3}$��
�ߡ�OPA=��B=90�㣬
���ADP�ס�PCO��
��AD��PC=DP��CO��
��8��y=y��CO��
��AC=$\frac{{y}^{2}}{8}$=$\frac{8}{3}$��
��OB=8-$\frac{8}{3}$=$\frac{16}{3}$��
��AB=2y=$\frac{16\sqrt{3}}{3}$��
��tan��OAB=$\frac{OB}{AB}$$\frac{\frac{16}{3}}{\frac{16\sqrt{3}}{3}}$=$\frac{\sqrt{3}}{3}$��
���OAB=30�㣻
���OAP=��DAP=30�㣬
�ߡ�OPA=��D=90�㣬
���ADP�ס�APO��
���ɢٿ�֪AB=$\frac{16\sqrt{3}}{3}$��
��2���ߡ�ADP�ס�PCO����OCP���PDA�������Ϊ1��4��
��$\frac{DP}{CO}$=$\frac{2}{1}$����DP=2CO��$\frac{AD}{PC}$=$\frac{2}{1}$��AD=2PC��
��AD=8��
��PC=4��
��RT��ADP��AP2=AD2+DP2��
��AP=DC=AB��
��AB2=64+��AB-4��2�����AB=10��
�ڡ�GP=6-t��PH=2t�����GPH�ĸ�Ϊh������h=$\frac{AD}{AP}$•2t=$\frac{8}{5}t$��
��S�ı���ADGH=S��ADP-S��GHP=$\frac{1}{2}$DP•DA-$\frac{1}{2}$GP•h=$\frac{1}{2}$��8��6-$\frac{1}{2}$����6-t����$\frac{8}{5}$t=$\frac{4}{5}$��t-3��2+$\frac{84}{5}$��
�൱t=3ʱ���ı���ADGH�����S����СֵΪ$\frac{84}{5}$��
���� ������Ҫ�����������ε��ۺ��⣬�õ���֪ʶ�������������ε��ж������ʡ�ȫ�������ε��ж������ʡ����ɶ��������������ε����ʣ��ؼ������������ߣ��ҳ�ȫ�Ⱥ����Ƶ������Σ�


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
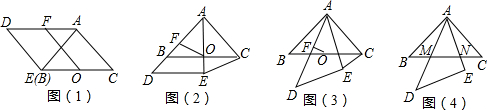
 ��ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����E��F�ֱ����߶�AO��BO���е㣮��AC+BD=24���ף���OAB���ܳ���20���ף���EF=4���ף�
��ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����E��F�ֱ����߶�AO��BO���е㣮��AC+BD=24���ף���OAB���ܳ���20���ף���EF=4���ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��۲���ȷ���ǣ�������
���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��۲���ȷ���ǣ�������| A�� | b2-4ac��0 | B�� | ��-1��x��3ʱ��y��0 | ||
| C�� | c��0 | D�� | ��x��1ʱ��y��x����������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
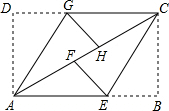 ��ͼ��ABCD�Ǿ���ֽƬ�����ۡ�B����D��ʹBC��ADǡ������AC�ϣ���F��H�ֱ���B��D����AC�ϵ����㣮E��G�ֱ����ۺ�CE��AG��AB��CD�Ľ��㣮����GF��HE����AB=4cm��BC=3cm�����ı���GFEH���������$\frac{3}{2}$cm2��
��ͼ��ABCD�Ǿ���ֽƬ�����ۡ�B����D��ʹBC��ADǡ������AC�ϣ���F��H�ֱ���B��D����AC�ϵ����㣮E��G�ֱ����ۺ�CE��AG��AB��CD�Ľ��㣮����GF��HE����AB=4cm��BC=3cm�����ı���GFEH���������$\frac{3}{2}$cm2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��Rt��AEF����Rt��ABC��ת���ɵģ�����ת�����ǵ�A����ת�Ƕ��ǡ�BAE���CAF��
��ͼ��Rt��AEF����Rt��ABC��ת���ɵģ�����ת�����ǵ�A����ת�Ƕ��ǡ�BAE���CAF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
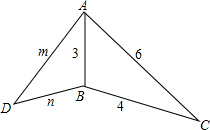 ��ͼ��ʾ����ABC�ס�DBA����m=$\frac{9}{2}$��n=$\frac{9}{4}$��
��ͼ��ʾ����ABC�ס�DBA����m=$\frac{9}{2}$��n=$\frac{9}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
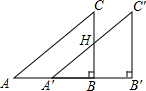 ��Rt��ABC��ֱ��AB����ƽ��2����λ�õ�Rt��A��B��C�䣬��AB=4����ABC=90�㣬��S��ABC=6����S�ı���BB��C��H��
��Rt��ABC��ֱ��AB����ƽ��2����λ�õ�Rt��A��B��C�䣬��AB=4����ABC=90�㣬��S��ABC=6����S�ı���BB��C��H���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com