
在△ABC中,AC=25,AB=35,tanA=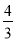 ,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
(1)如图1,当DF⊥AB时,求AE的长;
(2)如图2,当点E、F在边AB上时,求y关于x的函数关系式,并写出函数的定义域;
(3)联结CE,当△DEC和△ADF相似时,求x的值.
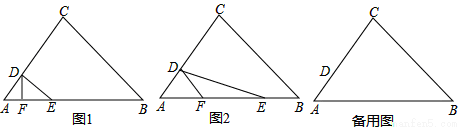
(1) 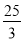 ,(2) y=6-
,(2) y=6-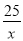 (
(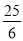 ≤x≤35);(3) x=25或x=5或x=
≤x≤35);(3) x=25或x=5或x=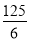 .
.
【解析】
试题分析:(1)先根据DF⊥AB,∠EDF=∠A,得出∠ADE=90°,再根据AD=5,tanA=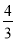 ,即可求出AE;
,即可求出AE;
(2)过点D作DG⊥AB,交AB于G,先证出△EDF∽△EAD,得出ED2=AE•EF,再求出DG、AG,最后根据EG=x-6,DE2=42+(x-3)2得出42+(x-3)2=x•(x-y),再进行整理即可;
(3)先证出∠AFD=∠EDC,再分两种情况讨论:①当∠A=∠CED时,得出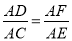 ,
,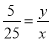 ,再把y=6-
,再把y=6-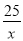 代入得出5(6-
代入得出5(6-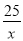 )=x,再解方程即可;②当∠A=∠DCE时,根据△ECD∽△DAF得出
)=x,再解方程即可;②当∠A=∠DCE时,根据△ECD∽△DAF得出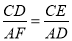 ,
,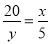 ,再把y=6-
,再把y=6-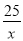 代入得出5(6-
代入得出5(6-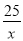 )=x,求出方程的解即可.
)=x,求出方程的解即可.
试题解析:(1)∵DF⊥AB,
∴∠AFD=90°,
∴∠A+∠ADF=90°
∵∠EDF=∠A,
∴∠EDF+∠ADF=90°,
即∠ADE=90°,
在Rt△ADE中,∠ADE=90°,AD=5,tanA=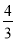
∴DE=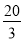 ,
,
∴AE=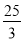 ,
,
(2)过点D作DG⊥AB,交AB于G,
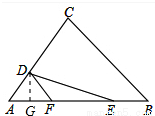
∵∠EDF=∠ADE,∠DEF=∠AED,
∴△EDF∽△EAD,
∴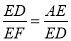 ,
,
∴ED2=AE•EF,
∴RT△AGD中,∠AGD=90°,AD=5,tanA=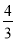 ,
,
∴DG=4,AG=3,
∴EG=x-3,
∴DE2=42+(x-3)2,
∴42+(x-3)2=x•(x-y),
∴y=6-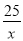 (
(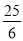 ≤x≤35);
≤x≤35);
(3)∵∠A+∠AFD=∠EDF+∠EDC,且∠EDF=∠A,
∴∠AFD=∠EDC,
①当∠A=∠CED时,
∵∠EDF=∠A,
又∵∠CED=∠FDE,
∴DF∥CE
∴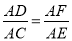 ,
,
∴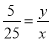
∵y=6-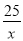 ,
,
∴5(6-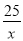 )=x,
)=x,
x1=25,x2=5;
②当∠A=∠DCE时,
∵∠EDF=∠A,
∴△ECD∽△DAF
∴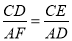 ,
,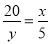 ,
,
∵y=6-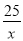 ,
,
∴5(6-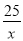 )=x,
)=x,
∴x=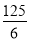 ,
,
∴当△DEC和△ADF相似时,x=25或x=5或x=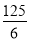 .
.
考点:相似形综合题.


科目:初中数学 来源:2013-2014学年上海市虹口区中考二模数学试卷(解析版) 题型:解答题
如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,BC=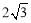 .
.
(1)求AB的长;
(2)求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市浦东新区中考二模数学试卷(解析版) 题型:选择题
某粮食公司2013年生产大米总量为a万吨,比2012年大米生产总量增加了10%,那么2012年大米生产总量为
(A) 万吨 (B)
万吨 (B)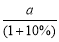 万吨;
万吨;
(C)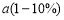 万吨 (D)
万吨 (D)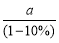 万吨.
万吨.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市毕业生学业模拟考试数学试卷(解析版) 题型:选择题
顺次连结等腰梯形的各边中点所得到的四边形是( )
(A)平行四边形 (B)菱形 (C)矩形 (D)正方形
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市松江区中考二模数学试卷(解析版) 题型:填空题
在等腰梯形、正五边形、平行四边形、矩形这4种图形中,任取一种图形,这个图形是中心对称图形的概率是
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市杨浦区5月中考二模数学试卷(解析版) 题型:解答题
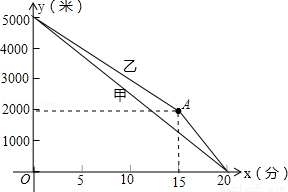
甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:
(1)他们在进行 米的长跑训练,在0<x<15的时段内,速度较快的人是 ;
(2)求甲距终点的路程y(米)和跑步时间x(分)之间的函数关系式;
(3)当x=15时,两人相距多少米?在15<x<20的时段内,求两人速度之差.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市普陀区中考二模数学试卷(解析版) 题型:选择题
下列命题中,错误的是( )
A.三角形重心是三条中线交点 B.三角形外心到各顶点距离相等
C.三角形内心到各边距离相等 D.等腰三角形重心、内心、外心重合
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com