
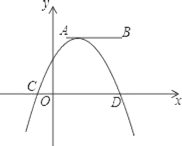
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为_____.
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,斜坡与教学楼剖面在同一平面内,已知斜坡CD的长为6m,坡度i=1:0.75,教学楼底部到斜坡底部的水平距离AC=8m,在教学楼顶部B点测得斜坡顶部D点的俯角为46°,则教学楼的高度约为( )
(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04).

A.12.1mB.13.3m
C.16.9mD.18.1m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个![]() 奖品和2个
奖品和2个![]() 奖品共需120元;购买5个
奖品共需120元;购买5个![]() 奖品和4个
奖品和4个![]() 奖品共需210元.
奖品共需210元.
(1)求![]() ,
,![]() 两种奖品的单价;
两种奖品的单价;
(2)学校准备在获奖的2名男生3名女生中选两名同学参加县上的比赛,请问选中两名选手都是女孩的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师将“校园诗词大赛”所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下:
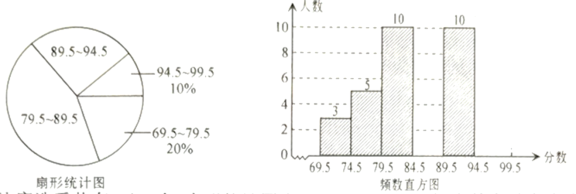
(1)本次比赛选手共有_ 人,扇形统计图中“![]() ”这一组人数占总参赛人数的百分比为_ ,频数直方图中“
”这一组人数占总参赛人数的百分比为_ ,频数直方图中“![]() ”这一组的人数为__ ;
”这一组的人数为__ ;
(2)赛前规定,成绩由高到低前![]() 的参赛选手获奖某参赛选手的比赛成绩为
的参赛选手获奖某参赛选手的比赛成绩为![]() 分,试判断他能否获奖,并说明理由;
分,试判断他能否获奖,并说明理由;
(3)成绩前四名是![]() 名男生和
名男生和![]() 名女生,若从他们中任选
名女生,若从他们中任选![]() 人作为全区“诗词大会”重点培训对象,试求恰好选中
人作为全区“诗词大会”重点培训对象,试求恰好选中![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
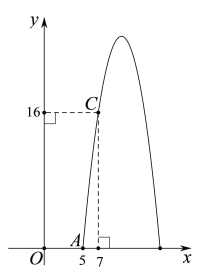
【题目】如图,某商品每天的销售利润![]() (元)与销售价
(元)与销售价![]() (元)之间满足函数
(元)之间满足函数![]() ,其图象与
,其图象与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在该图象上,点
在该图象上,点![]() ,
,![]() 的坐标见图所示.
的坐标见图所示.
(1)求出这个函数的解析式;
(2)销售价为多少元时,该商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“在已知三角形的一边上取一点,使得这点到这个三角形的另外两边的距离相等”的尺规作图过程:
已知:△ABC.
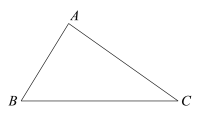
求作:点D,使得点D在BC边上,且到AB,AC边的距离相等.
作法:如图,
作∠BAC的平分线,交BC于点D.则点D即为所求.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形 (保留作图痕迹);
(2)完成下面的证明.
证明:作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴ = ( ) (填推理的依据) .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com