
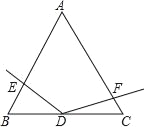
����Ŀ����ͼ����ABC�DZ߳�Ϊ4�ĵȱ������Σ���D���߶�BC���е㣬��EDF��120�㣬��
��EDF�Ƶ�D��ת��ʹ��EDF�����߷ֱ����߶�AB��AC���ڵ�E��F��
��1����DF��ACʱ����֤��BE��CF��
��2������ת�����У�BE+CF�Ƿ�Ϊ��ֵ�����ǣ���������ֵ�������ǣ���˵�����ɣ�
��3������ת�����У�����EF����BE��x����DEF�����ΪS����S��x֮��ĺ�������ʽ������S����Сֵ��
���𰸡���1������������2��BE+CF��2����Ϊ��ֵ����3��S��![]() ��x��1��2
��x��1��2![]() ����x��1ʱ��S��СֵΪ
����x��1ʱ��S��СֵΪ![]() .
.
��������
��1�������ı����ڽǺ�Ϊ360�㣬�����DEA��90�㣬���ݡ�AAS�����ж���BDE�ա�CDF������֤BE��CF��
��2������D��DM��AB��M����DN��AC��N����ͼ2����֤��MBD�ա�NCD������BM��CN��DM��DN��������֤����EMD�ա�FND������EM��FN���Ϳɵõ�BE+CF��BM+EM+CF��BM+FN+CF��BM+CN��2BM��2BD��cos60�㣽BD��![]() BC��2��
BC��2��
��3������F��FG��AB��������ɵ�S��DEF��S��ABC��S��AEF��S��BDE��S��BCF�������S��x֮��ĺ�������ʽ�����ݶ��κ�����ֵ��������S����Сֵ��
��1���ߡ�ABC�DZ߳�Ϊ4�ĵȱ������Σ���D���߶�BC���е㣬
���B����C��60�㣬BD��CD��
��DF��AC��
���DFA��90�㣬
�ߡ�A+��EDF+��AFD+��AED��180�㣬
���AED��90�㣬
���DEB����DFC���ҡ�B����C��60�㣬BD��DC��
���BDE�ա�CDF��AAS��
��2������D��DM��AB��M����DN��AC��N��
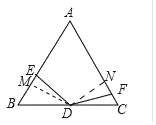
���С�AMD����BMD����AND����CND��90�㣮
�ߡ�A��60�㣬
���MDN��360�㩁60�㩁90�㩁90�㣽120�㣮
�ߡ�EDF��120�㣬
���MDE����NDF��
�ڡ�MBD�͡�NCD�У�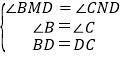
���MBD�ա�NCD��AAS��
BM��CN��DM��DN��
�ڡ�EMD�͡�FND�У�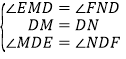 ��
��
���EMD�ա�FND��ASA��
��EM��FN��
��BE+CF��BM+EM+CF��BM+FN+CF��BM+CN
��2BM��2BD��cos60�㣽BD��![]() BC��2
BC��2
��3������F��FG��AB������ΪG��
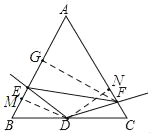
��BE��x
��AE��4��x��CF��2��x��
��AF��2+x��
��S��DEF��S��ABC��S��AEF��S��BDE��S��BCF��
��S��![]() BC��AB��sin60�㩁
BC��AB��sin60�㩁![]() AE��AF��sin60�㩁
AE��AF��sin60�㩁![]() BE��BD��sin60�㩁
BE��BD��sin60�㩁![]() CF��CD��sin60��
CF��CD��sin60��
��4![]() ��
��![]() ����4��x������2+x����
����4��x������2+x����![]() ��
��![]() ��x��2��
��x��2��![]() ��
��![]() ����2��x����2��
����2��x����2��![]()
��S��![]() ��x��1��2+
��x��1��2+![]() ��
��
�൱x��1ʱ��S��СֵΪ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ǧ����ǰ���ҹ���ѧ��ī�Ӻ�����ѧ������С�׳����ʵ�飮���������ǣ���һ��ڰ��������һ��ǽ�Ͽ�һ��С�ף�С�����ǽ�Ͼͻ�������澰��ĵ���С����ѧϰ��С�׳����ԭ����������ͼװ������֤С�׳����������֪һ����ȼ�������С��20 cm�������ھ�С��30 cm����С������������Ļ���߶�Ϊ2 cm��������ϻ���������ĸ߶�Ϊ__________ cm.
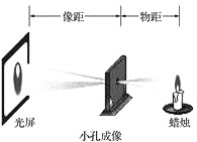
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲�����ֱ���AB�ĸ߶���ij�ۺ�ʵ��С���ڵ���D����ֱ���ñ��CD�����ڵ�����ˮƽ���ø�ƽ�澵E��ʹ��B��E��D��ͬһˮƽ��������ͼ��ʾ.��С���ڱ�˵�F��ͨ��ƽ�澵Eǡ�ù۲��˶�A(��ʱ��AEB=��FED).��F�������˶�A������Ϊ39.3�㣬ƽ�澵E�ĸ���Ϊ45�㣬FD=1.8���������AB�ĸ߶�ԼΪ������? (�����������)(�ο�������tan39.3���0.82��tan84.3���10.02)
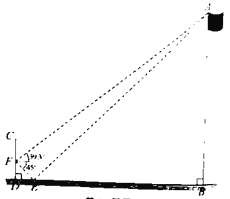
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����BAC=120����D��E��BC�ϵ����㣬�ҡ�DAE=30��������AEC�Ƶ�A˳ʱ����ת120���õ���AFB������DF.���н�������ȷ�ĸ����У�������
�١�FBD=60�����ڡ�ABE�ס�DCA����AEƽ�֡�CAD���ܡ�AFD�ǵ���ֱ��������.
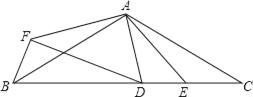
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
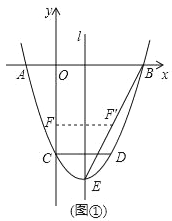
����Ŀ����ͼ�����κ���y=x2+bx+c��ͼ����x�ύ�� A��B���㣬��y�ύ�ڵ�C��OB=OC����D�ں���ͼ���ϣ�CD��x�ᣬ��CD=2��ֱ��l�������ߵĶԳ��ᣬE�������ߵĶ��㣮
��1����b��c��ֵ��
��2����ͼ�٣�����BE���߶�OC�ϵĵ�F����ֱ��l�ĶԳƵ�F'ǡ�����߶�BE�ϣ����F�����ꣻ
��3����ͼ�ڣ�����P���߶�OB�ϣ�����P��x��Ĵ��߷ֱ���BC���ڵ�M���������߽��ڵ�N�����ʣ����������Ƿ���ڵ�Q��ʹ�á�PQN���APM�������ȣ����߶�NQ�ij�����С��������ڣ������Q�����ꣻ��������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y=ax2+bx+2��x�ύ��A��B���㣬��y�ύ�ڵ�C��AB=4������OBDC�ı�CD=1���ӳ�DC���������ڵ�E��
��1���������ߵĽ���ʽ��
��2����ͼ2����P��ֱ��EO�Ϸ��������ϵ�һ�����㣬����P��y���ƽ���߽�ֱ��EO�ڵ�G����PH��EO������ΪH����PH�ij�Ϊl����P�ĺ�����Ϊm����l��m�ĺ�����ϵʽ������д��m��ȡֵ��Χ���������l�����ֵ��
��3�������N�������߶Գ����ϵ�һ�㣬���������Ƿ���ڵ�M��ʹ����M��A��C��NΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д���������������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
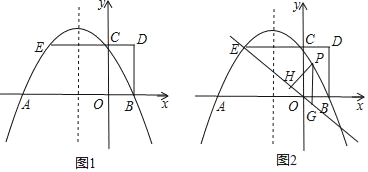
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=ax2+bx+c��a��0��ͼ���һ���֣������ߵĶ�������A��1��3������x���һ������B��4��0����ֱ��y2=mx+n��m��0���������߽���A��B���㣬���н��ۣ�
��2a+b=0����abc��0��������ax2+bx+c=3��������ȵ�ʵ����������������x�����һ�������ǣ���1��0��������1��x��4ʱ����y2��y1��
������ȷ���ǣ� ��

A. �٢ڢ� B. �٢ۢ� C. �٢ۢ� D. �ڢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������һ������С�������ɽ������ɽ������ɽ���Ĺ���������;��Ϣ��һ��ʱ����������ɽ�ų��������õ�ʱ��Ϊt�������������ߵ�·��Ϊs��������s��t֮��ĺ�����ϵ��ͼ��ʾ������˵������������ ��

A��С����;��Ϣ����20����
B��С����Ϣǰ��ɽ��ƽ���ٶ�Ϊÿ����70��
C��С�����������������ߵ�·��Ϊ6600��
D��С����Ϣǰ��ɽ��ƽ���ٶȴ�����Ϣ����ɽ��ƽ���ٶ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
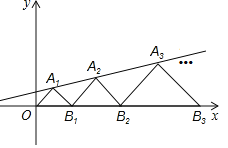
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A1��A2��A3������B1��B2��B3�����ֱ���ֱ��y=![]() x+b��x���ϣ���OA1B1����B1A2B2����B2A3B3�������ǵ���ֱ�������Σ������A1��1��1������ô��A2018����������_____��
x+b��x���ϣ���OA1B1����B1A2B2����B2A3B3�������ǵ���ֱ�������Σ������A1��1��1������ô��A2018����������_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com